样本数量和临界距离
样本数量 n 和临界距离 k 的计算取决于给定的规格限数量以及标准差是否已知。
单个规格限和已知的标准差
样本数量的计算公式如下:
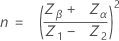
临界距离的计算公式如下:

其中:
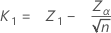
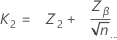
表示法
| 项 | 说明 |
|---|---|
| Z1 | (1 – p1) * 标准正态分布的第 100 个百分位数 |
| p1 | 可接受质量水平 (AQL) |
| Z2 | (1 – p2) * 标准正态分布的第 100 个百分位数 |
| p2 | 可拒收质量水平 (RQL) |
| Zα | (1 – α) * 标准正态分布的第 100 个百分位数 |
| α | 生产者风险 |
| Zβ | (1 – β ) * 标准正态分布的第 100 个百分位数 |
| β | 消费者风险 |
单个规格限和未知的标准差
表示法与单个规格限和已知标准差部分中的表示法相同。样本数量的计算公式如下:
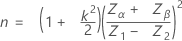
临界距离的计算公式如下:
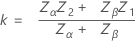
两个规格限和已知的标准差
对于单个规格限和已知的标准差,下面未定义的表示法相同。首先,Minitab 计算 z:
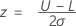
然后,Minitab 从标准正态分布中查找 p* 并将其作为与 z 相对应的上尾区域。这是在其中一个规格限外部出现不良品的最小概率。
Minitab 用于计算样本数量和临界距离的方法取决于这个 p* 值。
设 p1 = AQL,p2 = RQL
- 如果 2p* ≤ (p1/ 2),则两个规格离得相对较远,计算将服从单个限制计划。
- 如果 p1/ 2 < 2p* ≤ p1,则两个规格离得相对不远,但是没有近到可以针对某些均值找到最小不良品概率的地步。Minitab 执行迭代来查找样本数量和临界距离。
设
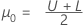
μ = μ0+ m * h,其中 h = σ/100
设 m = 1, 2, ...300。对于每个 μ,计算:

其中 Φ 是标准正态分布的累积分布函数。如果 Prob (X<L) + Prob (X>U) 与 p1 特别接近,则 Minitab 使用 Prob (X<L) 和 Prob (X>U) 之间较大的值来查找样本数量和验收数。
假设 Prob (X<L) 是较大的值,设 pL = Prob (X<L)。
样本数量的计算公式如下:
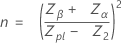
临界距离的计算公式如下:

其中:

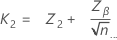
ZpL = (1 – pL) * 标准正态分布的第 100 个百分位数。
如果我们已经使用了所有的 m 值,但相应的概率不包含 p1,则 p1 太大,这意味着测量的平均值远离区间中点 [L,U]。在这种情况下,我们可以使用单个规格限的方法和 ZpL = Z1。Z1 的定义与单个规格限案例的定义相同。
- 如果 p1 < 2p* < p2,则必须考虑计划的规格,因为由两个规格限确定的不良品最小概率和标准差比可接受质量水平 p1 大。可以拒绝批次,或者考虑使用不良品概率稍大于 p1 的计划。
- 如果 2p* ≥ p2,则应当拒收该批次;由两个规格限确定的不良品最小概率和标准差比可拒收的质量水平大。您可以不检验任何产品就拒绝该批次。
表示法
| 项 | 说明 |
|---|---|
| L | 规格下限 |
| U | 规格上限 |
| σ | 已知的标准差 |
两个规格限和未知的标准差(默认程序)
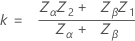
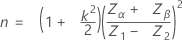
- 设
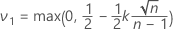
- 则,

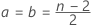 。
。 - 定义
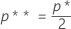
- 则,
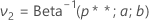
-

-

如果 n ≤ 2,则无法计算最大标准差 (MSD)。
两个规格限和未知的标准差(Wallis 程序)
表示法与前面部分中的表示法相同。以下程序可以在 Schilling 的书籍中找到。2
首先,Minitab 设临界距离等于在提供两个不同限制计划时给出的值:
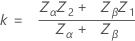
然后,Minitab 从对应于 k(作为百分位数)的标准正态分布查找上尾区域 p*,从对应于 p* / 2 上尾区域的标准正态分布查找百分位数 Zp**。
最大标准差 (MSD) 的计算公式如下:
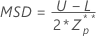
估计标准差的计算公式如下:
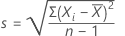
Minitab 检验估计标准差 s 是否小于或等于 MSD。
如果估计标准差 s 小于或等于平均偏差平方和,则样本数量由以下公式提供:
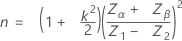
如果估计标准差 s 大于 MSD,则说明标准差太大,与验收标准不一致,您必须拒收该批次。
表示法
| 项 | 说明 |
|---|---|
| Xi | 第 i 个测量值 |
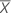 | 实际测量值的均值 |
验收概率
假设 p 是缺陷概率,等于 OC 曲线上某个点的 x 值。
单个规格限和已知的标准差
- 单个规格下限和已知的标准差
- Prob (X < L) = p。
- 单个规格上限和已知的标准差
- Prob (X > L) = p。
单个规格限和未知的标准差

两个规格限和已知的标准差
首先,Minitab 计算 z

然后,Minitab 从标准正态分布中查找 p* 并将其作为与 z 相对应的上尾区域。这是在其中一个规格限外部出现缺陷品的最小概率。
Minitab 用于计算验收概率的方法取决于这个 p* 值。
设 p1 = AQL,p2 = RQL
- 如果 2p* ≤ (p1/2),则两个规格离得相对较远,样本数量和临界距离的计算将服从单个限制计划。
- 如果 p1/ 2 < 2p* ≤ p1,则两个规格离得相对不远,但是没有近到可以针对某些均值找到最小缺陷品概率的地步。
对于任何给定的 p,Minitab 使用网格搜索算法查找测量值的均值 μ。然后,
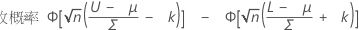
两个规格限和未知的标准差
当您拥有规格上限和规格下限,但不知道标准差时,Minitab 使用单限值计划的 OC 曲线来接近双规格限情况。为指定了 p1、p2、α 和 β 的单限值计划派生的 OC 曲线是具有相同 p1、p2、α 和 β 的双侧规格计划的 OC 曲线上规格带的下限,对于大多数实际情况,可被视为双侧计划的 OC 曲线。请参见 Duncan1。
- Duncan (1986)。Quality Control and Industrial Statistics(质量控制和行业统计量),第 5 版。
表示法
| 项 | 说明 |
|---|---|
| n | 样本数量 |
| k | 临界距离 |
| σ | 已知的标准差 |
| Zp | 标准正态分布中第 (1 - p) 个百分位点 |
| Φ | 标准正态分布的累积分布函数 |
| T |
自由度为 n – 1 的非中心 t 分布,非中心参数 |
| L | 规格下限 |
| U | 规格上限 |
拒收概率
拒收概率 (Pr) 描述基于特定的抽样计划和进厂缺陷品比率拒收特定批次的概率。它等于 1 减去验收概率。
Pr = 1 – Pa
其中:
Pa = 验收概率
平均检出质量 (AOQ)
平均检出质量表示在检验之后产品的质量水平。平均检出质量因进厂缺陷品率不同而异。
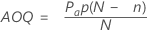
表示法
| 项 | 说明 |
|---|---|
| Pa | 验收概率 |
| p | 进厂缺陷品率 |
| N | 批次大小 |
| n | 样本数量 |
平均总检验数 (ATI)
平均总检验数表示在特定进厂质量水平和验收概率下将检验的平均单位数。

表示法
| 项 | 说明 |
|---|---|
| Pa | 验收概率 |
| N | 批次大小 |
| n | 样本数量 |
验收区域 (AR) - 默认程序
只有当给定两种规格而标准差未知时,才计算验收区域。请转到有关样本数量和临界距离的部分,分别查找 n 和 k 的定义并查看方程的表示法。
在验收区域图中,x 轴是样本均值,y 轴是样本标准差。验收区域由 3 个与样本标准差和样本均值相关的函数,以及最大标准差 (MSD) 形成。对于其处的样本标准差值超过 MSD 的任何样本均值,验收区域的上限为 MSD。
对于接近规格上限或下限的情形,验收区域由以下两个函数限定:
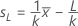

- 设
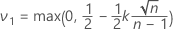 。
。 - 则
 其中,Beta 是具有形状参数 a 和 b 的 beta 分布的累积分布函数。这里,
其中,Beta 是具有形状参数 a 和 b 的 beta 分布的累积分布函数。这里,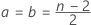 。
。 - 定义可满足 p02 + p01 = p* 的比率对 p01 和 p02
- 接着,


- 对于
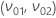 ,均值和标准差的坐标符合以下方程:
,均值和标准差的坐标符合以下方程:
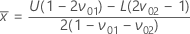
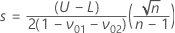
验收区域 (AR) - Wallis 程序
当分析同时具有两个规格但标准差未知时,则采用以下计算。这个程序可以在 Schilling 的书籍中找到。2
 ),y 轴显示标准差的值。与 x 轴组合,下面的线构成一个验收三角形。
),y 轴显示标准差的值。与 x 轴组合,下面的线构成一个验收三角形。


虚线和 x 轴形成一个更准确的区域。可使用以下步骤来形成虚线。
- 设 p* 为标准正态分布的上尾区域,临界距离为百分位数:P(Z > k)。
- 选择满足 p02 + p01 = p* 的 p01 和 p02 值:
- p01 = (p* / 100) * h
- p02 = (p* / 100) * (100 - h)
其中 h 取值范围为 1 到 00。
- 使用以下方程来定义 X 和 Y 坐标:
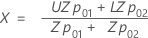
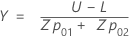
表示法
| 项 | 说明 |
|---|---|
| L | 规格下限 |
| U | 规格上限 |
| k | 临界距离 |
| Zp01 | 标准正态分布中的第 (1 - p01)* 100 个百分位数 |
| Zp02 | 标准正态分布中的第 (1 - p02)* 100 个百分位数 |
| p01 | (p* / 100) * h |
| p02 | (p* / 100) * (100 – h) |



