什么是 Poisson 分布?
Poisson 分布由一个参数指定:lambda (λ)。此参数等于均值和方差。当 lambda 增大到足够大的值时,正态分布 (λ, λ) 可用于接近 Poisson 分布。
使用 Poisson 分布描述在有限观测空间内的事件发生次数。例如,Poisson 分布可以描述飞机机械系统中的缺陷数或呼叫中心的一小时来电数。Poisson 分布通常用在质量控制、可靠性/生存研究和保险中。
当满足以下条件时,变量服从 Poisson 分布:
- 数据是事件的计数(没有上限的非负整数)。
- 所有事件都是独立的。
- 平均比率不随相关时间段而改变。
下图显示了具有不同 lambda 的 Poisson 分布。
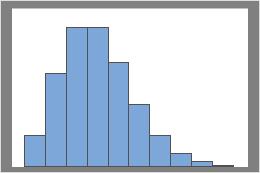
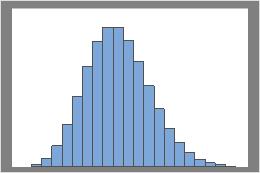

Lambda = 3

Lambda = 10
什么是发生率?
发生率等于均值 (λ) 除以观测空间维度。它对于比较在不同观测空间中收集的 Poisson 计数非常有用。例如,总机 A 在 5 小时内接到 50 通来电,而总机 B 在 10 小时内接到 80 通来电。您无法直接比较这些值,因为它们的观测空间不同。您必须计算发生率来比较这些计数。总机 A 的发生率为(50 通来电/5 小时) = 10 通来电/小时。总机 B 的发生率为(80 通来电/10 小时) = 8 通来电/小时。
Poisson 分布与二项分布之间的区别
Poisson 分布与二项分布类似,因为它们都为事件计数建模。但是,在其有限观测空间内,Poisson 分布不对计数设置上限:总机可在一天中接到无限数量的电话而不违反 Poisson 分布的要求。相反,二项式分布会对计数设置上限:您观测的事件数不能大于您执行的试验次数。
