什么是超几何分布?
超几何分布是在知道样本所源自的总体中的项总数时,可对固定样本数量中的事件数量建模的离散分布。样本中每个项都具有两种可能的结果(事件或非事件)。样本没有被替换,因此,样本中的每个项都是不同的。在从总体中选择项后,就不能再次选择该项了。因此,项被选中的几率会随着每一次试验不断增加(如果尚未选择此特定项)。
在不进行替换的情况下,超几何分布可用于从相对较小的总体中提取的样本。例如,超几何分布用在 Fisher 精确检验中以检验两个比例之间的差异,并按属性抽样验收,以从有限大小的孤立批次中进行抽样。
超几何分布由以下 3 个参数定义:总体大小、总体中的事件计数以及样本数量。
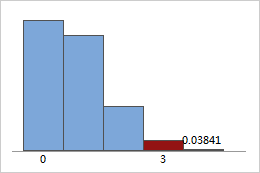
计算超几何概率的示例
假设有 10 辆车可供您试驾 (N = 10),其中 5 辆配有涡轮增压发动机 (x = 5)。如果您试驾其中三辆车 (n = 3),那么这三辆车中的两辆配有涡轮增压发动机的概率是多少?
- 选择。
- 选择概率。
- 在总体大小 (N)中,输入 10。在 总体中的事件计数 (M) 中,输入 5。在 样本数量 (n) 中,输入 3。
- 选择输入常量并输入 2。
- 单击 确定。
在试驾十辆车中感兴趣的三辆车时,随机挑选两辆具有涡轮发动机的汽车的概率是 41.67%。
超几何分布与二项分布的区别
超几何分布和二项分布都描述了在固定试验数中事件发生的次数。对于二项分布,每个试验的概率是相同的。对于超几何分布,每次试验都会改变每次后续试验的概率,因为不存在替换。
对具有以下特点的总体使用二项分布:数量特别大,使得试验结果对后续结果是事件还是非事件的概率几乎没有影响。例如,在含 100,000 人的总体中,53,000 人具有 O+ 型血。样本中第一个随机选择的人具有 O+ 型血的概率是 0.530000。如果样本中的第一个人具有 O+ 型血,则第二个人具有 O+ 型血的概率是 0.529995。这些概率之间的差别特别小,足以在大多数应用中忽略。
对具有以下特点的总体使用超几何分布:数量特别小,使得试验结果对后续结果是事件还是非事件的概率具有很大影响。例如,在含 10 人的总体中,7 人具有 O+ 型血。样本中第一个随机选择的人具有 O+ 型血的概率是 0.700000。如果样本中的第一个人具有 O+ 型血,则第二个人具有 O+ 型血的概率是 0.66667。此差值可随样本数量增加而增大。这些概率之间的差别特别大,无法在大多数应用中忽略。
