可使用指数分布对连续 Poisson 过程中的两个事件之间的时间进行建模。假设独立事件以恒定速率发生。
此分布应用广泛(包括产品和系统的可靠性分析、排队理论以及马尔可夫链)。
例如,指数分布可用于对以下内容进行建模:
- 电子元件的失效时间
- 客户到达终端的间隔时间
- 客户排队等待的服务时间
- 拖欠付款的时间(信用风险建模)
- 放射性核衰变的时间
2 参数指数分布由其尺度和阈值参数定义。如果阈值参数 θ 为正数,则将分布向右偏移距离 θ。例如,您对研究 θ = 5 的系统失效非常感兴趣。这意味着仅在操作 5 小时后才开始出现失效,之前不会出现失效。在下图中,阈值参数 θ 等于 5,它将分布向右偏移 5 个单位。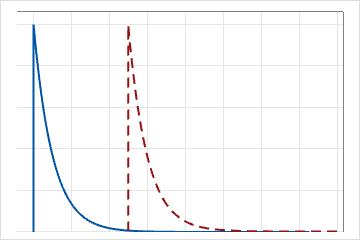

对于 1 参数指数分布,阈值为零,且分布由其尺度参数定义。对于 1 参数指数分布,尺度参数等于均值。
无记忆的含义是什么?
指数分布的重要属性为它是无记忆的。事件的发生机会不依赖于过去的试验。因此,发生率保持不变。
该无记忆属性指示元件的剩余寿命与其当前使用年限无关。例如,抛硬币的随机试验体现了无记忆属性。经过磨损并在使用年限后期更容易失效的系统便不是无记忆的。
