什么是概率密度函数 (PDF)?
概率密度函数可帮助确定随机变量值的较高和较低概率的区域。
离散 PDF 的示例
对于离散变量,PDF 将给出给定 x 值的概率值。例如,糖果制造商生产多种颜色的某一类型糖果。生产的糖果中有 30% 为黄色,10% 为橙色,10% 为红色,20% 为绿色,30% 为蓝色。
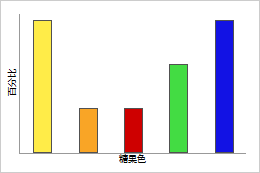

离散 PDF
此条形图显示了糖果颜色的 PDF。每个条形均表示以百分比表示的该颜色糖果的概率。
连续 PDF 的示例
概率密度函数 (PDF) 是一个用于表示连续随机变量的概率分布的等式。例如,为葡萄酒瓶切割软木塞的机器可产生直径不同的软木塞。在下面的软木塞直径条形图中,每个条形表示具有相应直径的软木塞的百分比。
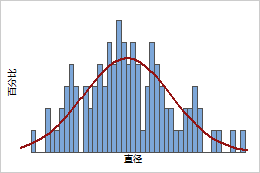

连续 PDF
曲线是软木塞直径的 PDF。可使用 PDF 确定随机变量值的较高和较低概率的范围。例如,只有较小百分比的软木塞 (1%) 直径小于 2.8 厘米。

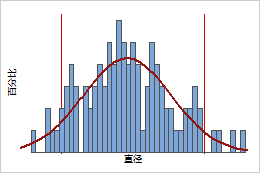
具有规格限的连续 PDF
如果软木塞直径的规格限为 2.85 厘米到 3.15 厘米,PDF 可指示此过程生产的满足规格的所有软木塞的概率密度值。
广为熟知的钟形曲线表示正态分布的 PDF。尽管软木塞直径服从正态分布,但其他测量值(如将软木塞从酒瓶中拔出所需的力)可能服从其他分布。例如,对数正态分布的 PDF 有一个长的右尾。例如,对数正态分布的 PDF 有一个长的右尾。
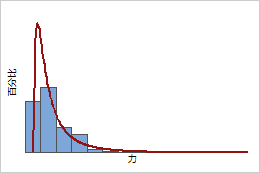

对数正态 PDF
由于有时需要很大的力才能从酒瓶上拔出软木塞,因此该力的度量通常服从具有长右尾的分布,如对数正态分布。
