什么是逆累积分布函数 (ICDF)？
逆累积分布函数给出与特定累积概率关联的值。可使用逆 CDF 确定与特定概率相关联的变量值。
使用 ICDF 确定保修期的示例
例如，一家电器制造商要调查其烤箱内加热管的失效时间。他们想要确定特定百分比的加热管失效的时间，以便设定保修期限。加热管的失效时间服从正态分布，其均值为 1000 小时，标准差为 300 小时。概率密度函数 (PDF) 可帮助确定较高和较低失效概率的范围。逆累积分布函数给出每个累积概率的对应失效时间。
使用逆累积分布函数估计 5% 的加热管失效所需的时间，95% 的加热管开始失效以及全部失效所需的时间，或仅剩 5% 加热管未失效的时间。特定累积概率的逆累积分布函数等于概率密度函数曲线下阴影区域右侧的失效时间。
确定 5% 的加热管失效所需的时间
- 选择。
- 选择逆累积概率。在均值中，输入 1000。在标准差中，输入 300。在输入常量中，输入 0.05。
- 单击确定。
5% 的加热管失效所需的时间预计为 0.05 倍的逆累积分布函数或 506.544 小时。
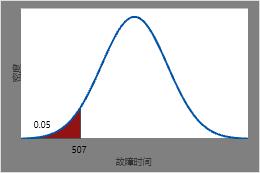
此图说明逆累积分布函数。
确定 95% 的加热管失效所需的时间
- 选择。
- 选择逆累积概率。在均值中，输入 1000。在标准差中，输入 300。在输入常量中，输入 0.025。单击确定。
2.5% 的加热管失效所需的时间预计为 0.025 倍的逆累积分布函数或 412 小时。
- 重复步骤 2，但输入 0.975 而非 0.025。单击确定。97.5% 的加热管失效所需的时间预计为 0.975 倍的逆累积分布函数或 1588 小时。
因此，95% 的加热管开始失效和全部失效所需的时间预计分别为 0.025 倍和 0.975 倍的逆累积分布函数或 412 小时和 1588 小时。
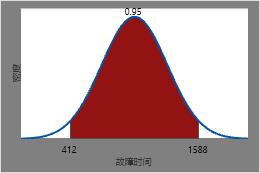
此图说明逆累积分布函数。
确定 5% 的加热管未失效的时间
- 选择。
- 选择逆累积概率。在均值中，输入 1000。在标准差中，输入 300。在输入常量中，输入 0.95。
- 单击确定。
仅剩 5% 的加热管未失效的时间预计为 .95 倍的逆累积分布函数或 1493 小时。
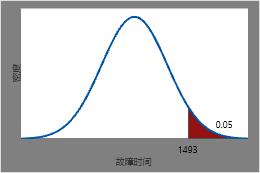
此图说明逆累积分布函数。
将 CDF 和 ICDF 与超几何分布结合使用的示例
在尝试确定离散分布的逆累积概率时，输出结果中将包含两组列。
假设某个比率的逆累积概率为 p。输出内容中第一组列将列出最大的 x，使 P(X ≤ x) ≤ p。第二组列将列出最小的 x，使 P(X ≤ x) ≥ p。
计算超几何分布的累积概率
- 在工作表的 C1 列中，输入 0 1 2。
C1 0 1 2 - 选择。
- 选择累积概率。
- 在总体大小 (N)中，键入 20000。
- 在总体中的事件计数 (M)中，键入 2000。
- 在样本数量 (n)中，键入 20。
- 选择输入列并输入 C1。单击确定。
累积分布函数
- P(X ≤ 0) = 0.121448。获得 0 个缺陷的概率大约为 12%。
- P(X ≤ 1) = 0.391619。获得 0 或 1 个缺陷的概率大约为 39%。
- P(X ≤ 2) = 0.676941。获得 0、1 或 2 个缺陷的概率大约为 68%。
计算超几何分布的逆累积概率
现在，您知道了与缺陷数相关联的累积概率，可以计算逆累积概率了。
假设您要计算缺陷数 x，使累积概率 p 为 0.50。通过前面的结果了解到，P(X ≤ 1 ) = 0.391619 并且 P(X ≤ 2 ) = 0.676941。由于超几何分布是一种离散分布，缺陷数无法介于 1 和 2 之间。换言之，可以有 1 个或 2 个缺陷，但不会有 1.4 个缺陷。因此，如果选择输入常量并输入 0.50，则 Minitab 将会在输出中计算这两个概率，如以下示例所示：
- 选择。
- 选择逆累积概率。
- 在总体大小 (N)中，键入 20000。
- 在总体中的事件计数 (M)中，键入 2000。
- 在样本数量 (n)中，键入 20。
- 选择输入常量，并键入 0.50。单击确定。
逆累积分布函数
第一个概率指示 x 的值，使 P(X ≤ x) < p；第二个概率指示最小的 x，使 P(X ≤ x) ≥ p。在该示例中，第一个概率显示最大缺陷数 x = 2，使 P(X ≤ 2) < 0.5；第二个概率显示最小缺陷数 x = 3，使 P(X ≤ 3) ≥ 0.5。
使用 ICDF 计算临界值
可以使用 Minitab 计算一个假设检验的临界值，而不用在表格中查找该值。
假设您在 α = 0.02、自由度等于 12 的情况下执行卡方检验。对应的临界值是多少？α = 0.02 所对应累积概率值为 1 – 0.02 = 0.98。
- 选择。
- 选择逆累积概率。
- 在自由度中，输入 12。
- 选择输入常量并输入 0.98。
- 单击确定。
Minitab 显示临界值 24.054。对于卡方检验，如果检验统计量大于临界值，则可以断定存在否定原假设的统计学证据。
注意
此示例使用卡方分布。但是，您可以为所选择的任何分布执行相同的步骤。
