累积分布函数 (CDF) 计算给定 x 值的累积概率。可使用 CDF 确定取自总体的随机观测值将小于或等于特定值的概率。
使用 CDF 评估填充重量的示例
例如,罐装苏打水的填充重量服从正态分布,且均值为 12 盎司,标准差为 0.25 盎司。概率密度函数(PDF)描述了填充重可能值的概率。CDF提供了每个x值的累积概率。
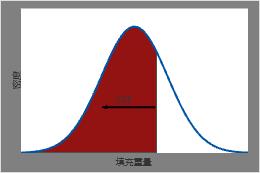
任意特定点处的填充重量的 CDF 等于 PDF 曲线下直至该点左侧的阴影面积。
使用 CDF 可以确定随机选择的罐装苏打水的填充重量小于 11.5 盎司、大于 12.5 盎司或介于 11.5 到 12.5 盎司之间的概率。
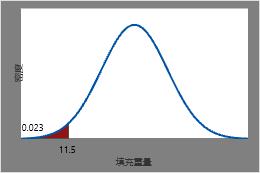
随机选择的罐装苏打水的填充重量小于或等于 11.5 盎司的概率为 11.5 处的 CDF,或大约 0.023。
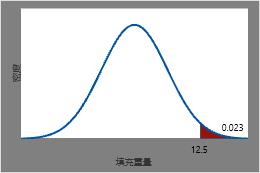
随机选取的汽水罐装重大于12.5盎司的概率为1减去12.5的CDF(0.977),约为0.023。
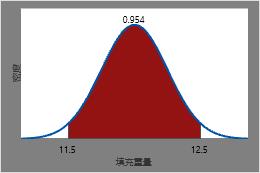
随机选择的罐装苏打水的填充重量介于 11.5 到 12.5 盎司之间的概率为 12.5 处的 CDF 减去 11.5 处的 CDF,或大约 0.954。
使用 CDF 计算 p 值
为了计算F检验的p值,首先必须计算累积分布函数(CDF)。p值为1 – CDF。
假设你进行具有以下自由度的多重线性回归分析:DF(回归)= 3;DF(误差)= 25;F -统计量 = 2.44。
计算 F 检验的 p 值
- 选择 。
- 选择累积概率。
- 在非中心参数中,输入 0。
- 在分子自由度中,输入 3。
- 在分母自由度中,输入 25。
- 选择 输入常量 并输入 2.44。
- 在可选存储中,输入 K1。单击 确定。 K1 包含累积分布函数。
使用“计算器”从 1 减去 p 值
- 选择 。
- 在 将结果存储在变量中中输入 P值。
- 在表达式中,输入 1-K1。单击 确定。
计算出的p值为0.08795。使用0.05的阈值,你不会得出统计显著性结论,因为0.08795不小于0.05。
注意
该示例适用于 F 分布;但是可针对其他分布使用类似的方法。
