什么是连续分布?
连续分布描述连续随机变量的可能值的概率。连续随机变量是具有一组无限且不可计数的可能值(称为范围)的随机变量。
连续随机变量 (X) 的概率被定义为其 PDF 曲线下的面积。因此,只有值范围才能具有非零的概率。连续随机变量等于某个值的概率始终为零。
重量分布示例
连续正态分布可以描述成年男性的体重分布。例如,可以计算男性体重为 160 到 170 磅之间的概率。
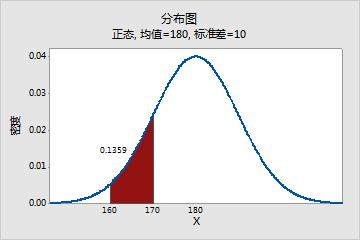
成年男性体重分布图
在此示例中,曲线下的阴影区域代表从 160 到 170 磅之间的范围。该范围的面积是 0.136;因此,随机选择的男性体重介于 160 和 170 英镑之间的概率为 13.6%。曲线下的整个面积等于 1.0。
但是,X 精确等于某个值的概率始终为零,因为曲线下单个点的面积为零(没有宽度)。例如,男子体重恰好为 190 磅(至无限精确)的概率为零。您可以计算男性体重超过 190 磅或小于 190 磅的概率,或者介于 189.9 到 190.1 磅之间的概率,但恰好等于 190 磅的概率为零。
什么是离散分布?
离散分布描述离散随机变量的每个值的发生概率。离散随机变量是指具有可计数的值的随机变量,例如非负整数的列表。
在离散概率分布中,离散随机变量的每个可能值可与一个非零概率相关联。因此,离散概率分布通常具有表格形式。
客户投诉数量示例
不同于连续分布,在离散分布中,您可以计算 X 恰好等于某个值的概率。例如,可以使用离散 Poisson 分布来描述一天内的客户投诉数量。假设平均每天的投诉数量为 10,并且您想知道在一天中接收 5、10、15 个客户投诉的概率。
| x | P (X = x) |
|---|---|
| 5 | 0.037833 |
| 10 | 0.12511 |
| 15 | 0.034718 |
您还可以查看分布图上的离散分布,以了解各范围之间的概率。
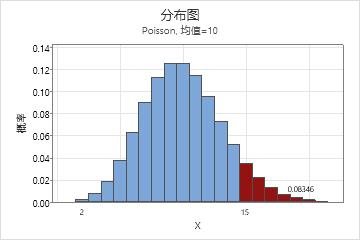

客户投诉数量分布图
在本示例中,带阴影的条形表示每天客户投诉数量为 15 或更多的次数。各条形高度的总和为 0.08346;因此,每天的呼叫数量为 15 或以上的概率是 8.35%。
