请完成以下步骤来解释双样本均值的随机化检验。主要输出包括直方图和 p 值。
步骤 1:检查自举分布的形状
使用直方图可以检查自举分布的形状。自举分布是每个重新采样样本的所选统计量的分布。自举分布看上去应当为正态分布。如果自举分布不是正态分布,您将无法信任自举结果。

50 个重新采样的样本

1000 个重新采样的样本
通常,重新采样的样本越多,越便于确定自举分布。例如,在这些数据中,对于 50 个重新采样样本,分布看上去不明确。对于 1000 个重新采样样本,分布形状看上去接近正态。
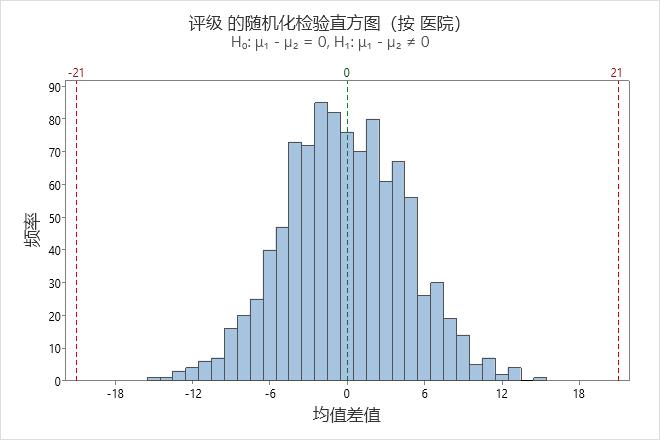
在该直方图中,自举分布看上去为正态分布。
步骤 2:确定检验结果在统计意义上是否显著
要确定总体均值的差值在统计意义上是否显著,请将 p 值与显著性水平进行比较。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在实际上不存在差异时得出存在差异的风险为 5%。
- P 值 ≤ α:均值的差值在统计意义上显著(否定 H0)
- 如果 p 值小于或等于显著性水平,则决策为否定原假设。您可以得出总体均值的差值在统计意义上显著的结论。要计算置信区间并确定差值实际上是否显著,请使用双样本均值引导。有关更多信息,请转到统计显著性和实际显著性。
- P 值 > α:均值的差值在统计意义上不显著(无法否定 H0)
- 如果 p 值大于显著性水平 0.05,则决策为无法否定原假设。您的证据不足,无法得出总体均值的差值在统计意义上显著的结论。
方法
| μ₁: 医院 = A 时 评级 的总体均值 |
|---|
| µ₂: 医院 = B 时 评级 的总体均值 |
| 差值: μ₁ - µ₂ |
观测到的样本
| 医院 | N | 均值 | 标准差 | 方差 | 最小值 | 中位数 | 最大值 |
|---|---|---|---|---|---|---|---|
| A | 20 | 80.30 | 8.18 | 66.96 | 62.00 | 79.00 | 98.00 |
| B | 20 | 59.30 | 12.43 | 154.54 | 35.00 | 58.50 | 89.00 |
观测到的均值差值
| A 的均值 - B 的均值 = 21.000 |
|---|
随机化检验
| 原假设 | H₀: μ₁ - µ₂ = 0 |
|---|---|
| 备择假设 | H₁: μ₁ - µ₂ ≠ 0 |
| 重新采样数 | 平均 | 标准差 | P 值 |
|---|---|---|---|
| 1000 | -0.185 | 4.728 | < 0.002 |
主要结果:P 值
在这些结果中,原假设声明两家医院的平均评级的差值为 0。由于 p 值小于 0.002,这小于显著性水平 0.05,因此决策为否定原假设并得出两家医院的评级不同的结论。
