直方图
直方图将样本值分成多个区间并使用条形表示每个区间中的数据值频率。
解释
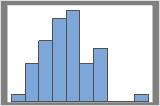
50 个重复样本
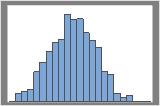
1000 个重复样本
通常,重复样本越多,该分布越易于确定。例如,在这些数据中,如果具有 50 个重复样本,则分布较模糊。如果具有 1000 个重复样本,则形状看上去大约为正态。
直方图可直观地显示假设检验的结果。随机化样本表示在总体均值相等时随机样本看起来是什么样的,因此直方图以 0 为中心。对于单侧检验,会在原始样本的均值之差处绘制参考线。对于双侧检验,会在原始样本的均值之差处和 0 对侧的相同距离处绘制参考线。P 值是比参考线处的值更极端的样本差值的比率。换言之,p 值为当假定原假设为真时如同原始样本一样极端的样本差值的比率。在直方图上,这些差值为红色。
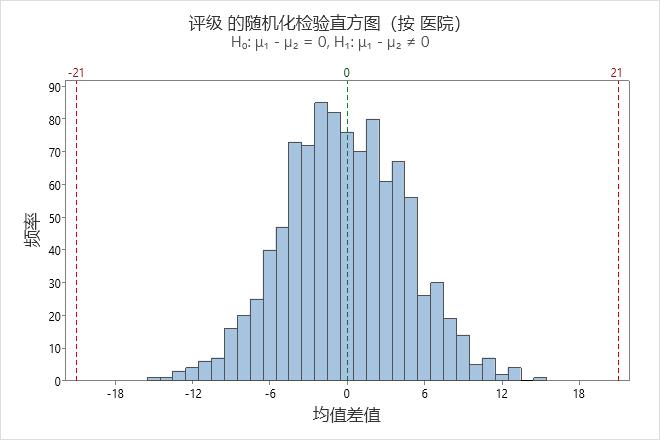
在此直方图中,自举分布显示为正态。任何样本差值均大于 21,也不小于 -21。
单值图
单值图显示样本中的单个值。每个圆形表示一个观测值。当您具有的观测值相对较少,以及需要评估每个观测值的效应时,单值图尤其有用。
注意
Minitab 会在仅执行一次重复抽样时显示单值图。Minitab 会同时显示原始数据和重复样本数据。
解释
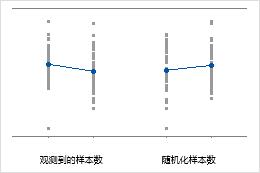
总体均值相等
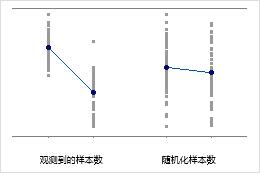
组 1 的总体均值是组 2 的总体均值的两倍
原假设和备择假设
- 原假设
- 原假设声明如均值、标准差等总体参数等于假设值。原假设通常是基于先前分析或专业知识的初始声明。
- 备择假设
- 备择假设声明总体参数小于、大于或不同于原假设中的假设值。备择假设是可能相信为真实或有望证明为真实的内容。
方法
| μ₁: 医院 = A 时 评级 的总体均值 |
|---|
| µ₂: 医院 = B 时 评级 的总体均值 |
| 差值: μ₁ - µ₂ |
观测到的样本
| 医院 | N | 均值 | 标准差 | 方差 | 最小值 | 中位数 | 最大值 |
|---|---|---|---|---|---|---|---|
| A | 20 | 80.30 | 8.18 | 66.96 | 62.00 | 79.00 | 98.00 |
| B | 20 | 59.30 | 12.43 | 154.54 | 35.00 | 58.50 | 89.00 |
观测到的均值差值
| A 的均值 - B 的均值 = 21.000 |
|---|
随机化检验
| 原假设 | H₀: μ₁ - µ₂ = 0 |
|---|---|
| 备择假设 | H₁: μ₁ - µ₂ ≠ 0 |
| 重新采样数 | 平均 | 标准差 | P 值 |
|---|---|---|---|
| 1000 | -0.185 | 4.728 | < 0.002 |
在这些结果中,原假设声明总体差值等于 0。备择假设声明该差值不等于 0。
重复样本数
重复样本数是指 Minitab 从原始数据集中进行替换性随机抽样的次数。通常,重复样本数较大时,效果最佳。每个重复样本的样本数量等于原始数据集的样本数量。重复样本数等于直方图上的观测值数。
平均值
平均值为随机化样本均值的所有差值之和除以重复样本数。Minitab 为均值的差值、观测样本的差值和自举分布的差值(平均值)显示两个不同的值。这两个值都是对总体均值之差的估计值,通常是类似的。如果这两个值的差值较大,则应该增大原始样本的样本数量。
标准差(自举样本)
标准差是离差的最常用度量,即数据从均值展开的程度。符号 σ(西格玛)通常用于表示总体的标准差,而 s 用于表示样本的标准差。对某一过程而言随机或合乎自然规律的变异通常称为噪声。对某一过程而言随机或合乎自然规律的变异通常称为噪声。由于标准差与数据采用相同的单位,因此它通常比方差更易于解释。
自举样本的标准差(也称为自举标准误)是均值之差的抽样分布的标准差估计值。
解释
使用标准差可以确定自举样本的差值从差值的总体均值展开的程度。标准差值越大,差值越分散。对于正态分布来说,好的经验法则是大约 68% 的值位于差值的总体均值的一个标准差范围内,95% 的值位于两个标准差范围内,99.7% 的值位于三个标准差范围内。
使用自举样本的标准差可确定自举样本的差值对总体均值之差的估计精确度。值越小,表明总体差值的估计值越精确。通常,标准差越大,总体差值的自举标准误就越大,估计值越不精确。样本数量越大,总体差值的自举标准误就越小,估计值越精确。
P 值
p 值是在假设原假设为真时,与原始样本一样极端的样本差值的比率。p 值越小,否定原假设的证据越充分。
解释
- P 值 ≤ α:均值的差值在统计意义上显著(否定 H0)
- 如果 p 值小于或等于显著性水平,则决策为否定原假设。您可以得出总体均值的差值在统计意义上显著的结论。要计算置信区间并确定差值实际上是否显著,请使用双样本均值的自举。有关更多信息,请转到统计显著性和实际显著性。
- P 值 > α:均值的差值在统计意义上不显著(无法否定 H0)
- 如果 p 值大于显著性水平 0.05,则决策为无法否定原假设。您的证据不足,无法得出总体均值的差值在统计意义上显著的结论。
