直方图
直方图将样本值分成多个区间并使用条形表示每个区间中的数据值频率。
解释
50 个重新采样的样本
1000 个重新采样的样本
通常,重新采样的样本越多,越便于确定自举分布。例如,在这些数据中,对于 50 个重新采样样本,分布看上去不明确。对于 1000 个重新采样样本,分布形状看上去接近正态。
直方图直观地显示假设检验的结果。Minitab 调整数据,以便重新采样样本的中心与假设均值相同。 对于单侧检验,会在原始样本的均值出绘制参考线。对于双侧检验,会在原始样本的均值处以及假设均值相反一侧相同距离处绘制参考线。p 值是比参考线处的值更极端的样本均值的比率。换句话说,p 值是在假设原假设为真时,与原始样本一样极端的样本均值的比率。在直方图上,这些均值为红色。
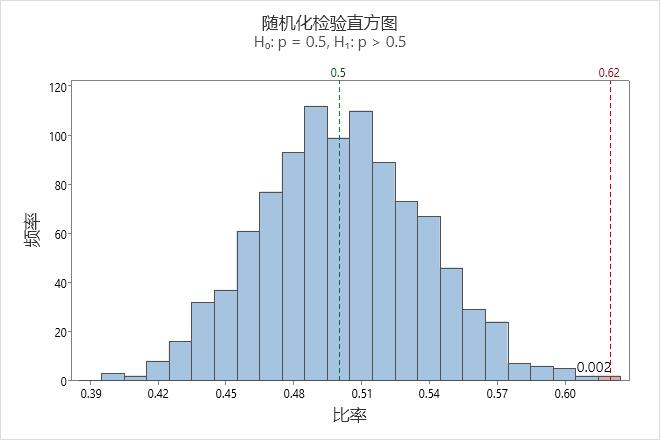
在此直方图中,自举分布显示为正态。如果 p 值为 0.002,则表示 0.2% 的样本比率大于原始样本的比率。
条形图
条形图显示每个类别的发生次数的比率。
注意
Minitab 会在仅执行一次重新采样时显示条形图。Minitab 既显示原始数据又显示重新采样数据。
解释
样本比率等于假设比率
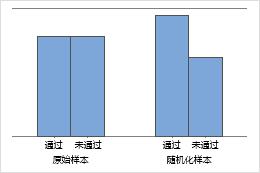
样本比率比假设比率低 20%
比率
样本比率等于事件数除以样本数量 (N)。
解释
Minitab 显示两个不同的比率值,观测样本的比率和自举分布的比率(平均值)。观测样本比率是对总体比率的估计值。自举分布的比率通常接近于假设比率。这两个值的差值越大,否定原假设的证据将越充分。
原假设和备择假设
- 原假设
- 原假设声明总体参数(如均值、标准差等)等于假设值。原假设通常是基于先前分析或专业知识的初始声明。
- 备择假设
- 备择假设声明总体参数小于、大于或不同于原假设中的假设值。备择假设是可能相信为真实或有望证明为真实的内容。
解释
在输出中,原假设和备择假设可帮助您验证是否为假设比率输入了正确的值。
观测到的样本
| N | 比率 |
|---|---|
| 200 | 0.620000 |
随机化检验
| 原假设 | H₀: p = 0.5 |
|---|---|
| 备择假设 | H₁: p > 0.5 |
| 重新采样数 | 平均 | P 值 |
|---|---|---|
| 1000 | 0.49942 | 0.002 |
在这些结果中,原假设声明总体比率等于 0.5。备择假设声明该比率大于 0.5。
重新采样的样本数
重新采样的样本数是 Minitab 从原始数据集随机抽取含替换内容的样本的次数。通常,重新采样的次数越多越好。
Minitab 调整数据,以便重新抽样样本的中心与假设比率相同。每个重新采样样本的样本数量等于原始数据集的样本数量。每个重新采样样本的数量等于直方图上的观测值数。
平均值
平均值为自助样本比率之和除以重复样本数。Minitab 会调整该数据,使重复样本的中心与假设比率相同。
解释
Minitab 显示两个不同的比率值,观测样本的比率和自助分布的比率(平均值)。观测样本比率是对总体比率的估计值。自助分布的比率通常接近于假设比率。这两个值的差值越大,否定原假设的证据将越充分。
P 值
P 值为当假定原假设为真时如同原始样本一样极端的样本比率的比率。p 值越小,否定原假设的证据越充分。
解释
使用 p 值可确定总体比率在统计意义上是否不同于假设比率。
- P 值 ≤ α:比率的差值在统计意义上显著(否定 H0)
- 如果 p 值小于或等于显著性水平,则决策为否定原假设。您可以得出总体比率与假设比率之间的差值在统计意义上显著的结论。要计算置信区间并确定差值实际上是否显著,请使用单样本函数引导。有关更多信息,请转到统计显著性和实际显著性。
- P 值 > α:比率的差值在统计意义上不显著(无法否定 H0)
- 如果 p 值大于显著性水平 0.05,则决策为无法否定原假设。您的证据不足,无法得出总体比率与假设比率之间的差值在统计意义上显著的结论。
