请选择您所选的方法或公式。
均值
一批数字的中心的常用度量。均值又称为平均数。均值是由所有观测值之和除以（非缺失）观测值个数得来的。
公式
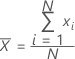
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
| N | 非缺失观测值个数 |
标准差 (StDev)
样本标准差用来度量数据的散布。它等于样本方差的平方根。
公式
如果列中包含 x 1, x 2,..., x N，且均值为 
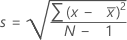
，则样本的标准差为：
，则样本的标准差为：
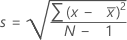
表示法
| 项 | 说明 |
|---|---|
| x i | 第 i 个观测值 |
 | 观测值的均值 |
| N | 非缺失观测值个数 |
方差
方差度量数据围绕其均值的分散程度。方差等于标准差的平方。
公式
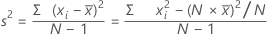
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
 | 观测值的均值 |
| N | 非缺失观测值个数 |
和
公式
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
最小值
数据集中的最小值。
中位数
样本中位数位于数据的中间：至少有一半的观测值小于或等于它，至少有一半的观测值大于或等于它。
假设您有一个包含 N 个值的列。要计算中位数，首先按照从小到大的顺序对数据值进行排序。如果 N 为奇数，则样本中位数是位于中间的值。如果 N 为偶数，则样本中位数是两个中间值的平均数。
例如，当 N = 5 且您有数据 x1、x2、x3、x4 和 x5 时，中位数 = x3。
当 N = 6 且您有排序数据 x1、x2、x3、x4、x5 和 x6 时：
其中 x3 和 x4 是第三个和第四个观测值。
最大值
数据集中的最大值。
均值（自举样本）
公式
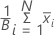
表示法
| 项 | 说明 |
|---|---|
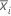 | 第 i 个重新采样样本的均值 |
| B | 重新采样的样本数 |
| N | 原始样本中的观测值数 |
自举分布的标准差
公式
表示法
| 项 | 说明 |
|---|---|
 | 重新采样的样本的均值 |
| B | 重新采样的样本数 |
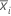 | 第 i 个重新采样样本的均值 |
P 值
公式
P 值的计算取决于备择假设。
- 均值小于假设值：
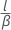
- 均值不等于假设值：
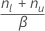
- 均值大于假设值：
表示法
| 项 | 说明 |
|---|---|
| l | 小于或等于样本均值的自举差值数 |
| u | 大于或等于样本均值的自举差值数 |
| β | 重新采样的样本数 |
| nl | 小于或等于 μ0 − d 的自举均值数 |
| nu | 大于或等于 μ0 + d 的自举均值数 |
| μ0 | 假设值 |
| d |  |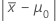
 | 观测样本的均值 |
