请完成以下步骤来解释单样本均值的随机化检验。主要输出包括直方图和 p 值。
步骤 1:检查自举分布的形状
使用直方图可以检查自举分布的形状。自举分布是每个重新采样样本的均值分布。自举分布看上去应当为正态分布。如果自举分布不是正态分布,您将无法信任结果。

50 个重新采样的样本

1000 个重新采样的样本
通常,重新采样的样本越多,越便于确定自举分布。例如,在这些数据中,对于 50 个重新采样样本,分布看上去不明确。对于 1000 个重新采样样本,分布形状看上去接近正态。
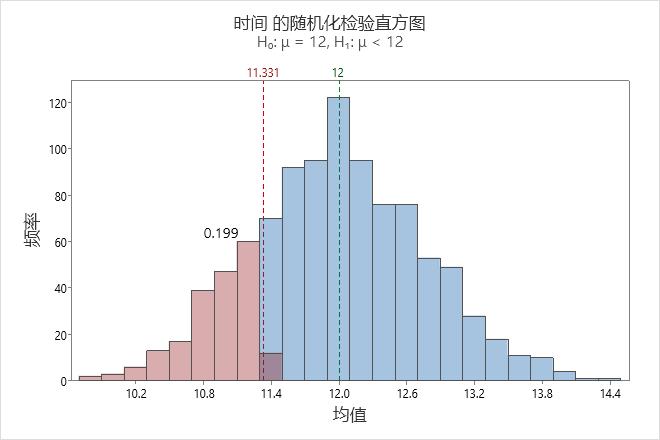
在该直方图中,自举分布看上去为正态分布。
步骤 2:确定检验结果在统计意义上是否显著
要确定总体均值和假设均值的差值在统计意义上是否显著,请将 p 值与显著性水平进行比较。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在实际上不存在差异时得出存在差异的风险为 5%。
- P 值 ≤ α:均值的差值在统计意义上显著(否定 H0)
- 如果 p 值小于或等于显著性水平,则决策为否定原假设。您可以得出总体均值与假设均值的差值在统计意义上显著的结论。要计算置信区间并确定差值实际上是否显著,请使用单样本函数引导。有关更多信息,请转到统计显著性和实际显著性。
- P 值 > α:均值的差值在统计意义上不显著(无法否定 H0)
- 如果 p 值大于显著性水平 0.05,则决策为无法否定原假设。您的证据不足,无法得出总体均值与假设均值之间的差值在统计意义上显著的结论。
观测到的样本
| 变量 | N | 均值 | 标准差 | 方差 | 和 | 最小值 | 中位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|
| 时间 | 16 | 11.331 | 3.115 | 9.702 | 181.300 | 7.700 | 10.050 | 16.000 |
随机化检验
| 原假设 | H₀: μ = 12 |
|---|---|
| 备择假设 | H₁: μ < 12 |
| 重新采样数 | 均值 | 标准差 | P 值 |
|---|---|---|---|
| 1000 | 11.9783 | 0.7625 | 0.199 |
主要结果:P 值
在这些结果中,备择假设声明反应时间均值小于 12 分钟。由于 p 值为 0.203,大于显著性水平 0.05,因此决策为无法否定原假设。您无法得出反应时间均值小于 12 分钟的结论。
