关于本主题
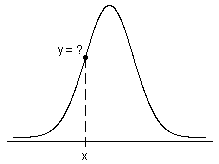
概率密度函数
- 对于连续分布,X 在区间 (a, b) 中具有值的概率是其在区间 (a, b) 中的 PDF 下的区域。
- 对于离散分布,X 在区间 (a, b) 中具有值的概率是 (a, b) 中 X 的可能离散值的 PDF(也称为概率密度函数)之和。
累积分布函数
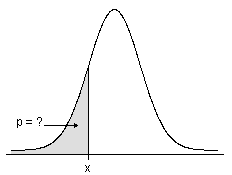
- 对于连续分布,CDF 给出概率密度函数下的区域,最多至您指定的 x 值。
- 对于离散分布,CDF 给出您指定的 x 值的累积概率。
逆累积概率
对于闭区间 [0,1] 中的数字 p,随机变量 X 的累积分布函数 (ICDF) 确定(在可能的情况下)一个值 x(使 X≤x 的概率大于或等于 p)。
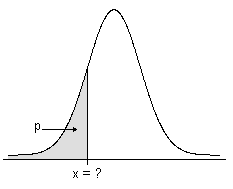
- 连续分布的 ICDF
-
ICDF 是与概率密度函数下的区域关联的值。ICDF 是累积分布函数 (CDF) 的反函数,累积分布函数是与某值相关联的区域。
对于所有连续分布,如果 0 < p < 1,则 ICDF 存在且唯一。
- 当概率密度函数 (PDF) 对整个实数行表示为正值(例如,正态 PDF)时,不会为 p = 0 或 p = 1 定义 ICDF。
- 当 PDF 对于大于某值的所有值表示为正值(例如卡方 PDF)时,将为 p =0 定义 ICDF,但不为 p =1 进行定义。
- 当 PDF 仅在某区间上才为正值时(例如,均匀 PDF),将为 p = 0 和 p = 1 定义 ICDF。
- 在未定义 ICDF 时,Minitab 会为结果返回一个缺失值 (*)。
- 离散分布的 ICDF
- 相比于连续分布,对应于离散分布的 ICDF 更复杂。例如,当使用 n = 5 且 p =..4 计算二项分布的 CDF 时,不存在使 CDF 为 ..5 的值 x。如果 x =1,CDF 为 ..3370。如果 x= 2,CDF 增大到 .6826。
Beta 分布
Beta 分布常用于表示具有自然上限和下限的过程。
公式
概率密度函数 (PDF) 是:

表示法
| 项 | 说明 |
|---|---|
| α | 形状参数 1 |
| β | 形状参数 2 |
| Γ | Gamma 函数 |
| a | 下限 |
| b | 上限 |
当 a = 0 时,b = 1,
PDF 为:
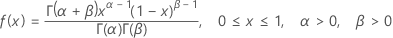


二项分布
二项分布用于表示在 n 个独立试验中发生的事件数。可能值包括从零到 n 的整数。
公式
均值 = np
方差 = np(1 – p)
概率质量函数 (PMF) 是:
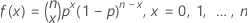
其中, 等于
等于  .
.
一般情况,可以使用 k! 作为 
表示法
| 项 | 说明 |
|---|---|
| n | 试验数 |
| x | 事件数 |
| p | 事件概率 |
Cauchy 分布
Cauchy 分布沿零对称,但其尾部接近零的速度要比正态分布慢。
公式
概率密度函数 (PDF) 是:
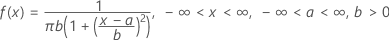
表示法
| 项 | 说明 |
|---|---|
| a | 位置参数 |
| b | 尺度参数 |
| π | Pi (~3.142) |
注意
如果不指定值,Minitab 使用 a = 0,b = 1。
卡方分布
如果 X 具有标准正态分布,X2 具有一个自由度为 1 的卡方分布,则允许它作为一个常用采样分布。
n 个独立 X2 变量(其中 X 具有标准正态分布)的总和具有卡方分布(自由度为 n)。卡方分布的形状取决于自由度的数量。
公式
概率密度函数 (PDF) 是:
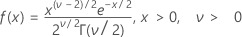
均值 = v
方差 = 2v
表示法
| 项 | 说明 |
|---|---|
| ν | 自由度 |
| Γ | Gamma 函数 |
| e | 自然对数的基数 |
离散分布
离散分布是您自己定义的一种分布。例如,假设您想了解一个由三个值 -1、0、1 组成的分布,其概率分别是 0.2、0.5 和 0.3。如果向工作表的列中输入值,则可以使用这些列来生成随机数据或计算概率。
| 值 | 概率 |
|---|---|
| −1 | 0.2 |
| 0 | 0.5 |
| 1 | 0.3 |
指数分布
可使用指数分布对故障间的间隔时间进行建模(例如,当单元具有恒定、瞬时的故障率(风险函数))。指数分布是 Weibull 分布和 Gamma 分布的一种特殊情况。
公式
概率密度函数 (PDF) 是:
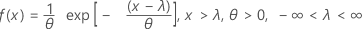
累积分布函数 (CDF) 是:

均值 = θ + λ
方差 = θ2
表示法
| 项 | 说明 |
|---|---|
| θ | 尺度参数 |
| λ | 阈值参数 |
| exp | 自然对数的基数 |
注意
一些参考使用 1/θ 作为参数。
F 分布
F 分布也称为方差比值分布,具有两种类型的自由度:分子自由度和分母自由度。它是两个独立的带有卡方分布的随机变量(每个变量被其自由度所除)的比值的分布。
公式
概率密度函数 (PDF) 是:
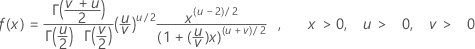

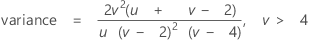
表示法
| 项 | 说明 |
|---|---|
| Γ | Gamma 函数 |
| u | 分子自由度 |
| v | 分母自由度 |
Gamma 分布
Gamma 分布通常用于对正向偏斜的数据建模。
公式
概率密度函数 (PDF) 是:

均值 = ab + θ
方差 = ab2
表示法
| 项 | 说明 |
|---|---|
| a | 形状参数(当 a = 1 时,Gamma PDF 与指数分布 PDF 相同) |
| b | 尺度参数 |
| θ | 阈值参数 |
| Γ | Gamma 函数 |
| e | 自然对数的基数 |
注意
一些参考使用 1/b 作为参数。
几何分布
离散几何分布适用于一系列独立 Bernoulli 试验(其中包含概率为 p 的相关事件)。
公式
如果随机变量 X 是生成一个事件(具有概率 p)所需执行的试验总次数,则 X 概率质量函数 (PMF) 由下式给出:

并且 X 显示以下属性:

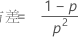
如果随机变量 Y 是在观测的第一个事件(具有概率 p)之前发生的非事件数,则 Y 的概率质量函数 (PMF) 由下式给出:

并且 Y 显示以下属性:

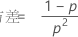
表示法
| 项 | 说明 |
|---|---|
| X | 生成一个事件所需执行的试验数, Y + 1 |
| Y | 在第一个事件之前发生的非事件数 |
| p | 事件在每个试验中的发生概率 |
超几何分布
在不进行替换的情况下,超几何分布可用于从较小的总体中提取的样本。例如,您有 N 台电视机,其中 N1 是优良品(成功),N2 是缺陷品(失败)。如果从 N 中随机采样 n 台电视机(不进行替换),您可以发现在 n 台电视机中概率 x 即为良好状态。
公式
概率质量函数 (PMF) 是:
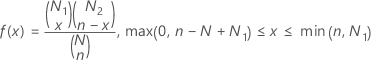


表示法
| 项 | 说明 |
|---|---|
| N | N1 + N2 = 总体大小 |
| N1 | 总体中的事件数 |
| N2 | 总体中的非事件数 |
| n | 样本数量 |
| x | 样本中的事件数 |
整数分布
整数分布是一组整数上的离散均匀分布。每个整数具有相同的出现概率。
正态分布
正态分布(也称为高斯分布)是最常使用的统计分布,因为此分布可对许多物理、生物和社会过程进行建模。
公式
概率密度函数 (PDF) 是:
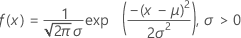
累积分布函数 (CDF) 是:
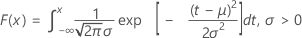
均值 = μ
方差 = σ 2
标准差 = σ
表示法
| 项 | 说明 |
|---|---|
| exp | 自然对数的基数 |
| π | Pi (~3.142) |
Laplace 分布
当与正态分布相比,分布的波峰更为尖锐时,将使用 Laplace 分布。
公式
概率密度函数 (PDF) 是:
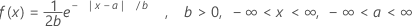
均值 = a
方差 = 2b2
表示法
| 项 | 说明 |
|---|---|
| a | 位置参数 |
| b | 尺度参数 |
| e | 自然对数的基数 |
最大极值分布
可使用最大极值分布对分布中的最大值进行建模。如果您具有一系列指数分布,并且 X(n) 是第 n 个分布中的最大值,则 X(n) – ln(n) 在分布中收敛于最大极值分布。因此,对于很大的 n 值,最大极值分布是 X(n) – ln(n) 的分布的充分近似。
公式
概率密度函数 (PDF) 是:

累积分布函数 (CDF) 是:

均值 = μ + γσ
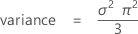
方差 = π 2 σ 2 / 6
表示法
| 项 | 说明 |
|---|---|
| σ | 尺度参数 |
| μ | 位置参数 |
| γ | Euler 常数 (~0.57722) |
Logistic 分布
一种对称的连续分布,与正态分布类似,但尾部更厚。
公式
概率密度函数 (PDF) 是:
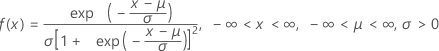
累积分布函数 (CDF) 是:
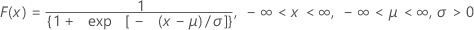
均值 = μ
表示法
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
对数 Logistic 分布
如果 Y = log (x – λ) 具有 logistic 分布,则变量 x 具有对数 Logistic 分布(阈值为 λ)。
公式
概率密度函数 (PDF) 是:
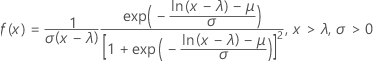
累积分布函数 (CDF) 是:

当 σ < 1:

当 σ < 1/2:
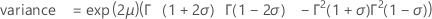
表示法
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
| λ | 阈值参数 |
| Γ | Gamma 函数 |
| exp | 自然对数的基数 |
对数正态分布
如果 log(x – λ) 具有正态分布,则变量 x 具有对数正态分布。
公式
概率密度函数 (PDF) 是:

累积分布函数 (CDF) 是:



表示法
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
| λ | 阈值参数 |
| π | Pi (~3.142) |
负二项分布
离散负二项分布适用于一系列独立 Bernoulli 试验(其中包含概率为 p 的事件)。
公式


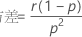
如果随机变量 Y 是在观测 r 个事件之前发生的非事件数(其中每个具有概率 p),则 Y 的概率质量函数 (PMF) 由下式给出:
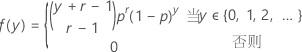
并且 Y 显示以下属性:

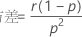
注意
负二项分布也称为 Pascal 分布。
表示法
| 项 | 说明 |
|---|---|
| X | Y + r |
| r | 事件数 |
| p | 事件的概率 |
Poisson 分布
Poisson 分布是可对基于恒定发生率的事件数量建模的离散分布。当独立试验数量大并且成功概率小时,Poisson 分布可用作二项式的近似。
公式
概率质量函数 (PMF) 是:
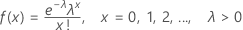
均值 = λ
方差 = λ
表示法
| 项 | 说明 |
|---|---|
| e | 自然对数的基数 |
最小极值分布
可使用最小极值分布对分布中的最小值进行建模。如果 Y 服从 Weibull 分布,则 log(Y) 服从最小极值分布。
公式
概率密度函数 (PDF) 是:
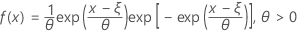
累积分布函数 (CDF) 是:



表示法
| 项 | 说明 |
|---|---|
| ξ | 位置参数 |
| θ | 尺度参数 |
| e | 自然对数的基数 |
| v | Euler 常数 (~0.57722) |
t 分布
- 创建正态分布中的总体均值的置信区间(当方差未知时)。
- 确定正态总体中的两个样本均值(具有未知但相等的方差)是否显著不同。
- 检验回归系数的显著性。
公式
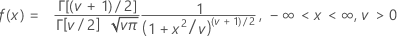
均值 = 0(当 ν > 0 时)

表示法
| 项 | 说明 |
|---|---|
| Γ | Gamma 函数 |
| v | 自由度 |
| π | Pi (~3.142) |
三角分布
三角分布的 PDF 具有一个三角形状。
公式
概率密度函数 (PDF) 如下所示:
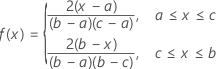

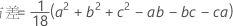
表示法
| 项 | 说明 |
|---|---|
| a | 下端点 |
| b | 上端点 |
| c | 模式(PDF 尖峰所在的位置) |
均匀分布
均匀分布的特征是数据在一个区间中均匀地分布,最小值为 a,最大值为 b。
公式
概率密度函数 (PDF) 是:

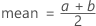
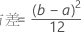
表示法
| 项 | 说明 |
|---|---|
| a | 下端点 |
| b | 上端点 |
Weibull 分布
Weibull 分布可对产品失效时间进行建模。
公式
概率密度函数 (PDF) 是:
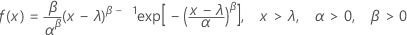
累积分布函数 (CDF) 是:

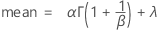
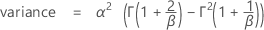
表示法
| 项 | 说明 |
|---|---|
| α | 尺度参数 |
| β | 形状参数,当 β = 1 时,Weibull PDF 与指数分布 PDF 相同 |
| λ | 阈值参数 |
| Γ | Gamma 函数 |
| exp | 自然对数的基数 |
注意
一些参考使用 1/α 作为参数。
