请完成以下步骤来解释双样本均值自举分析。主要输出包括直方图、平均值和置信区间。
步骤 1:检查自举分布的形状
使用直方图可以检查自举分布的形状。自举分布是每个重新采样样本的均值分布。自举分布看上去应当为正态分布。如果自举分布不是正态分布,您将无法信任结果。

50 个重新采样的样本

1000 个重新采样的样本
通常,重新采样的样本越多,越便于确定自举分布。例如,在这些数据中,对于 50 个重新采样样本,分布看上去不明确。对于 1000 个重新采样样本,分布形状看上去接近正态。
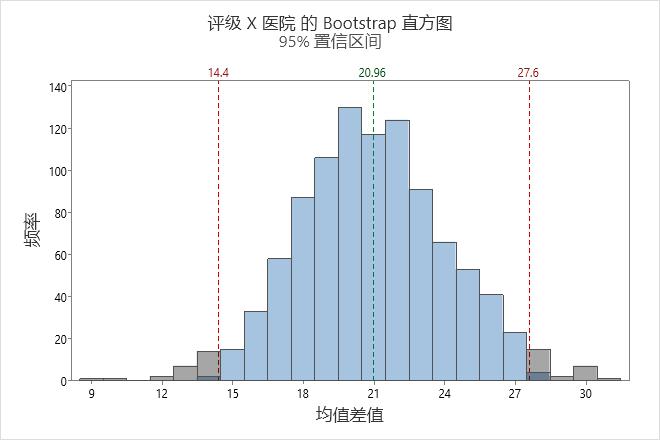
在该直方图中,自举分布看上去为正态分布。
步骤 2:确定总体均值的置信区间
首先考虑自举样本均值的差值,然后检查置信区间。
自举样本的均值差值是对总体均值中差值的估计值。由于自举样本的差值基于样本数据而不是整个总体,因此自举样本的差值不可能等于总体均值的差值。使用置信区间可以更好地估计总体均值的差值。
置信区间基于统计量的抽样分布。如果统计量不将偏倚作为参数的估计量,则它的抽样分布以参数的真实值为中心。自举分布接近统计量的抽样分布。因此自举分布的中间 95% 值为该参数提供 95% 置信区间。置信区间有助于估计总体参数估计值的实际显著性。使用您的专业知识可以确定置信区间是否包括对您的情形有实际显著性的值。
注意
当重新采样的样本数太小,以至于无法获取准确的置信区间时,Minitab 不计算置信区间。
观测到的样本
| 医院 | N | 均值 | 标准差 | 方差 | 最小值 | 中位数 | 最大值 |
|---|---|---|---|---|---|---|---|
| A | 20 | 80.30 | 8.18 | 66.96 | 62.00 | 79.00 | 98.00 |
| B | 20 | 59.30 | 12.43 | 154.54 | 35.00 | 58.50 | 89.00 |
观测到的均值差值
| A 的均值 - B 的均值 = 21 |
|---|
均值差值的 Bootstrap 样本
| 重新采样数 | 平均 | 标准差 | 差值的 95% 置信区间 |
|---|---|---|---|
| 1000 | 20.960 | 3.279 | (14.400, 27.600) |
主要结果:平均值、差值的 95% 置信区间
在这些结果中,总体差值的估计值为 20.96。总体差值介于 14.4 和 27.6 之间的可信度为 95%。
