直方图
直方图将样本值分成多个区间并使用条形表示每个区间中的数据值频率。
解释
50 个重新采样的样本
1000 个重新采样的样本
通常,重新采样的样本越多,越便于确定自举分布。例如,在这些数据中,对于 50 个重新采样样本,分布看上去不明确。对于 1000 个重新采样样本,分布形状看上去接近正态。
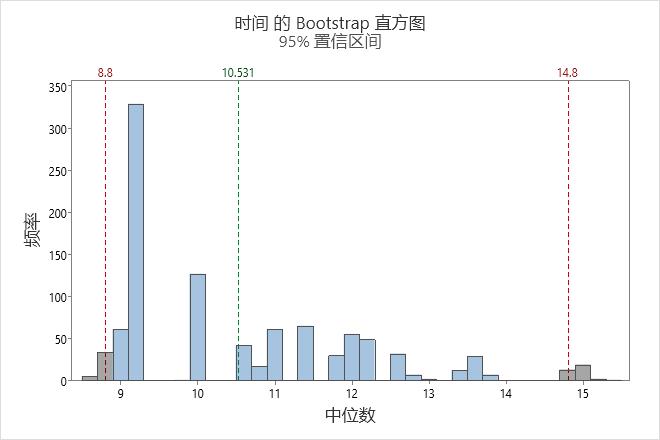
在该直方图中,自举分布看上去为正态分布。原始样本中仅有 16 个数据点。要获得可靠的置信区间,应当收集更大的样本并再次执行分析。
单值图
单值图显示样本中的单个值。每个圆形表示一个观测值。当您具有的观测值相对较少,以及需要评估每个观测值的效应时,单值图尤其有用。
注意
只有当您仅进行一次重新采样时,Minitab 才显示单值图。Minitab 既显示原始数据又显示重新采样数据。
解释
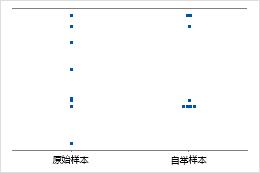
样本数量 8
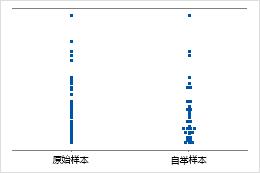
样本数量 50
条形图
条形图显示每个类别的出现次数的比率。
注意
只有当您仅进行一次重新采样时,Minitab 才显示条形图。 Minitab 既显示原始数据又显示重新采样数据。
解释
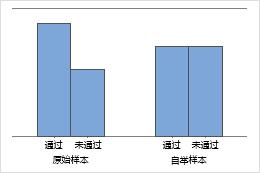
样本数量 8
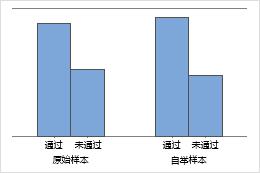
样本数量 50
重复样本数
重复样本数是指 Minitab 从原始数据集中进行替换性随机抽样的次数。通常,重复样本数较大时,效果最佳。每个重复样本的样本数量等于原始数据集的样本数量。重复样本数等于直方图上的观测值数。
平均值
平均值是自举样本中的所有统计量之和除以重新采样的样本数。
解释
Minitab 显示所选统计量的两个不同值:观测样本的值和自举分布的值(平均值)。 这两个值都是总体参数的估计值而且通常将相似。如果这两个值之间的差值很大,则应当增加原始样本的样本数量。
由于平均值基于样本数据而不是整个总体,因此平均值不可能等于总体参数。 使用置信区间可以更好地估计总体参数。
标准差(自举样本)
自举样本的标准差(又称为自举标准误)是所选统计量的抽样分布的标准差估计值
解释
使用标准差可以确定自举样本的所选统计量从总体均值扩散的程度。标准差值越大,数据越分散。
使用自举样本的标准差可以确定自举统计量对总体参数的估计精确度。标准参数的值越小,表明总体参数的估计值越精确。样本数量越大,自举标准误就越小,总体参数的估计值越精确。
置信区间 (CI) 和边界
置信区间基于统计量的抽样分布。如果统计量不将偏倚作为参数的估计量,则它的抽样分布以参数的真实值为中心。自举分布接近统计量的抽样分布。因此自举分布的中间 95% 值为该参数提供 95% 置信区间。置信区间有助于估计总体参数估计值的实际显著性。使用您的专业知识可以确定置信区间是否包括对您的情形有实际显著性的值。
注意
当重新采样的样本数太小,以至于无法获取准确的置信区间时,Minitab 不计算置信区间。
观测到的样本
| 变量 | N | 均值 | 标准差 | 方差 | 和 | 最小值 | 中位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|
| 时间 | 16 | 11.331 | 3.115 | 9.702 | 181.300 | 7.700 | 10.050 | 16.000 |
均值的 Bootstrap 样本
| 重新采样数 | 均值 | 标准差 | μ 的 95% 置信区间 |
|---|---|---|---|
| 1000 | 11.3095 | 0.7625 | (9.8562, 12.8562) |
在这些结果中,总体均值的估计值为 11.3。总体均值介于大约 9.9 和 12.9 之间的可信度为 95%。
