概率图通过根据其估计累积概率标绘每个观测值(包括重复的值),从样本创建估计的累积分布函数 (CDF)。
Minitab 通过使用以下公式之一,根据在中选择的内容(默认情况下选择中位数秩)计算估计的累积概率。对于每个公式,使 n 等于观测值个数,使 i 等于每个观测值的秩顺序,这样 i = 1 表示最小值,而 i = n 表示最大值。
- 中位数秩 (Benard)
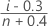
- 均值秩 (Herd-Johnson)

- 修正后 Kaplan-Meier (Hazen)
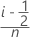
- Kaplan-Meier

注意
Kaplan-Meier 方法导致最大观测值的 p = 1。由于所得到的值不能用在图中,因此 Minitab 改为将最大的 p 计算为上一个 p 与 1 之间距离的 90%。
拟合分布线表示具有所指参数(估计参数或历史参数)的所选理论分布的 CDF。如果未提供历史参数,则 Minitab 将使用最小二乘估计(正态分布或对数正态分布)或极大似然估计(其他分布)来估计参数。
Y 值(在某些情况下是 X 值)将变换,以使拟合线为线性。但是,刻度标签始终与未变换值保持一致。因此,当所选分布与数据达到完全拟合的程度时,标绘点形成一条直线。
下表显示了对每种分布使用的变换。
| 分布 | X 坐标 | Y 坐标(分值) |
|---|---|---|
| 正态 | 数据 | |
| 对数正态 | ln(数据) | |
| 3 参数对数正态 | ln(数据 - 阈值) | |
| Gamma | ln(数据) | G-1(p), k |
| 3 参数 Gamma | ln(数据 - 阈值) | G-1(p), k |
| 指数 | ln(数据) | ln(-ln(1 - p)) |
| 双参数指数 | ln(数据 - 阈值) | ln(-ln(1 - p)) |
| 最小极值 | 数据 | ln(-ln(1 - p)) |
| Weibull | ln(数据) | ln(-ln(1 - p)) |
| 3 参数 Weibull | ln(数据 - 阈值) | ln(-ln(1 - p)) |
| 最大极值 | 数据 | -ln(-ln(p)) |
| Logistic | 数据 |
 |
| 对数 Logistic | ln(数据) |
 |
| 3 参数对数 Logistic | ln(数据 - 阈值) |
 |
重要信息
如果标绘未针对阈值调整的数据,则分布拟合不是由直线表明。
表示法
| 项 | 说明 |
|---|---|
| 数据 | 观测值的数据值 |
| In(x) | x 的自然对数 |
| 标准正态分布的逆 CDF 为 p 返回的值。 | |
| G-1(p),k | Gamma 分布(形状 = k 且尺度 = 1)的逆 CDF 为 p 返回的值。除非输入历史值,否则 Minitab 不会使用估计的形状参数。 |
