请完成以下步骤来解释概率分布图。主要输出包括 p 值、拟合分布线和估计的百分位数。
步骤 1：确定数据是否不服从分布
要确定数据是否服从分布，请将 p 值与显著性水平进行比较。通常，显著性水平（用 α 或 alpha 表示）为 0.05 即可。显著性水平 0.05 表示当数据实际上服从分布时，判定数据不服从分布的风险为 5%。
- P 值 ≤ α：数据不服从分布（否定 H0）
- 如果 p 值小于或等于显著性水平，则决策为否定原假设并得出数据不服从分布的结论。
- P 值 > α：无法得出数据不服从分布的结论（无法否定 H0）
- 如果 p 值大于显著性水平，则决策为无法否定原假设，因为没有足够的证据得出数据不服从分布的结论。但是，您无法得出数据服从分布的结论。
有关如何为检验指定不同分布和参数的信息，请转到拟合分布线。
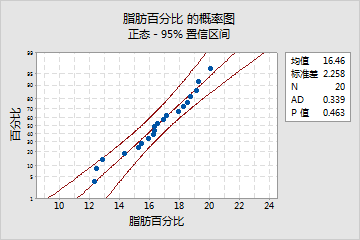
主要结果：P 值
在这些结果中，原假设声明数据服从正态分布。由于 p 值为 .463，大于显著性水平 .05，因此决策为无法否定原假设。您无法得出数据不服从正态分布的结论。
警告
样本数量影响检验功效。极小的样本可能会因功效不足而无法从分布中检测到显著的偏移。极大的样本可能因功效太大而从分布中检测到不重要的小偏移。因此，使用概率图上的直观结果以及 p 值可评估分布拟合，如步骤 2 中所示。
步骤 2：对分布的拟合程度进行可视化处理
检查概率图并评估数据点与拟合分布线的服从程度。如果指定的理论分布能够很好地拟合数据，则点将沿着直线紧密分布。例如，下面的正态概率图上的点沿拟合线分布。正态分布似乎能够很好地拟合数据。
注意
拟合分布线是图中间的直线。图上的外层实线是各个百分位数（而不是整个分布）的置信区间，不应当用来评估分布的拟合情况。
有关直观评估概率图上的值的更多信息，请转到正态概率图和“粗笔检验”。
步骤 3：显示总体估计百分位数
在 Minitab 中，将指针放在拟合分布线上可查看百分位数和值表。
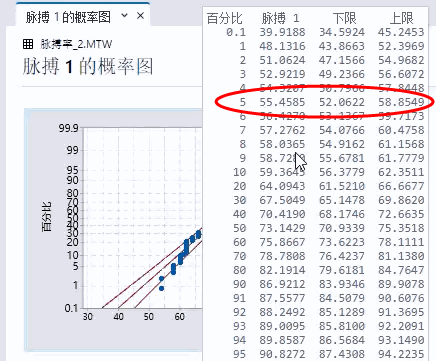
例如，下面的概率图显示检验对象在跑步机上走步时的脉搏率。对于均值和标准差等于该数据的正态分布，预计总体中有 5% 的脉搏率为 54.76 或更少。
注意
只有当数据紧密服从分布时，估计的总体百分位数才准确。
