和
和是所有数据值的合计。和还用在统计计算中,如用于计算均值和标准差。
均值
均值是数据的平均值,即所有观测值之和除以观测值的个数。
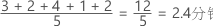
解释
使用均值来描述具有表示数据中心的单个值的样本。很多统计分析使用均值作为数据分布中心的一个标准度量。
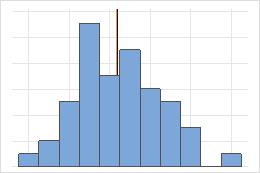
对称
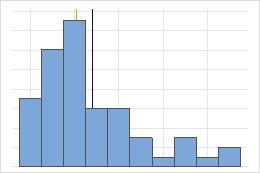
非对称
对于对称分布,均值(蓝线)和中位数(橙线)非常相似,以至于您很难区分这两条线。但是,非对称分布会向右偏斜。
标准差
标准差是离差的最常用度量,即数据从均值展开的程度。符号 σ(西格玛)通常用于表示总体的标准差,而 s 用于表示样本的标准差。对某一过程而言随机或合乎自然规律的变异通常称为噪声。对某一过程而言随机或合乎自然规律的变异通常称为噪声。
由于标准差与数据采用相同的单位,因此它通常比方差更易于解释。
解释
使用标准差可以确定数据从均值扩散的程度。 标准差值越大,数据越分散。 对于正态分布来说,好的经验法则是大约 68% 的值位于均值的一个标准差范围内,95% 的值位于两个标准差范围内,99.7% 的值位于三个标准差范围内。
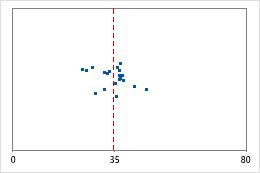
医院 1
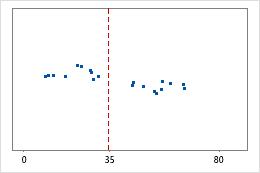
医院 2
医院出院时间
管理员对两家医院急诊部所治疗的患者的出院时间进行跟踪。尽管平均出院时间大致相同(35 分钟),但标准差显著不同。医院 1 的标准差大约为 6。平均而言,患者的出院时间大约偏离均值(虚线)6 分钟。医院 2 的标准差大约为 20。
最小值
最小值是最小的数据值。
在这些数据中,最小值为 7。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解释
使用最小值可以标识可能的异常值或数据输入错误。评估数据散布最简单的方法之一就是比较最小值和最大值。如果最小值非常低,甚至要考虑数据的中心、散布和形状,请调查出现极端值的原因。
最大值
最大值是指最大的数据值。
在这些数据中,最大值为 19。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解释
使用最大值可以标识可能的异常值或数据输入错误。评估数据散布最简单的方法之一就是比较最小值和最大值。如果最大值非常高,甚至要考虑数据的中心、散布和形状,请调查出现极端值的原因。
极差
极差是样本中的最大数据值与最小数据值之差。极差表示包含所有数据值的区间。
解释
使用极差可以了解数据的离差量。较大的极差值表示数据的离差较大。较小的极差值表示数据的离差较小。由于极差仅使用两个数据值进行计算,因此它对于小数据集更有用。
中位数
中位数是数据集的中点。在此中点值所在的点上,有一半的观测值大于中点值,有一半的观测值小于中点值。中位数是通过对观测值排秩并在秩顺序中查找第 [N + 1] / 2 位的观测值来确定的。如果观测值数为偶数,则中位数是排在第 N / 2 位和第 [N / 2] + 1 位的观测值的平均值。
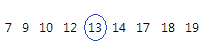
对于此排序数据,中位数是 13。也就是说,一半的值小于或等于 13,一半的值大于或等于 13。如果添加另一个等于 20 的观测值,则中位数为 13.5,即第 5 个观测值 (13) 和第 6 个观测值 (14) 的平均值。
解释

对称

非对称
对于对称分布,均值(蓝线)和中位数(橙线)非常相似,以至于您很难区分这两条线。但是,非对称分布会向右偏斜。
平方和
未校正平方和是通过对列中的每个值求平方来计算的,它计算这些平方值的和。例如,如果列中包含 x1, x2, ... , xn,则平方和等于 (x12 + x22 + ... + xn2)。与校正平方和不同的是,未校正平方和包括误差。在对数据值求平方之前不会先减去均值。
总计数
列中观测值的总数。用于表示 N 缺失和 N 非缺失之和。
| 总计数 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N
样本中非缺失值的个数。
| 总数 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N*
样本中缺失值的个数。缺失值个数是指包含缺失值符号 * 的单元格数。
| 总计数 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
