要使用这些函数，请选择 。
Gamma、不完整的 gamma 和 gamma 的自然对数函数是对因子函数 (1 * 2 * 3...* n) 的扩展，因此，除了针对正整数外，还可以针对分数计算因子。有时，在计算中使用 gamma 的自然对数函数，而不使用 gamma 函数，这是由于 gamma 的自然对数不太可能生成大于存储能力而且会导致溢出的极大数字。
语法
- GAMMA(形状)
- IGAMMA(极限,形状)
- LNGAMMA(形状)
对于形状，指定要带入函数的数字。对于极限，指定积分上限。
示例
| 计算器表达式 | 结果 |
|---|---|
| GAMMA(0.5) | 1.77245 |
| IGAMMA(1,2) | 0.264241 |
| LNGAMMA(3.5) | 1.20097 |
公式
完整的 Gamma 函数 
又称为广义阶乘函数，且定义如下：
又称为广义阶乘函数，且定义如下：
不完整的 Gamma 函数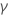 
是由具有有限（而不是无限）上限的积分定义的完整 Gamma 函数的变异。对于给定的数字 a 和上限 x，
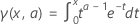
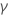是由具有有限（而不是无限）上限的积分定义的完整 Gamma 函数的变异。对于给定的数字 a 和上限 x，
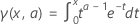
Gamma 的自然对数函数 
是完整 Gamma 函数的自然对数。
注意
当变量 a 等于负整数或零时，未定义完整的 Gamma 函数。当变量 a 等于任何负数或零时，未定义不完整的 Gamma 函数。当数字的 Gamma 函数未定义时，Minitab 将返回缺失值 *。
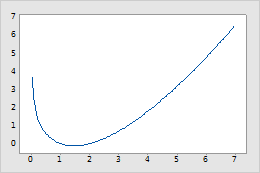
Lngamma 函数
Gamma 的自然对数是一个仅对正数定义的凸函数。
用途
Gamma 函数在理论数学和应用数学、科学以及工程（包括涉及到激光和人类组织中热传导的应用）中起着重要作用。在统计学中，gamma 函数用来计算 gamma 分布的概率密度函数和累积分布函数，gamma 分布用来描述正偏斜数据。
