In This Topic
Normal Probability Plot
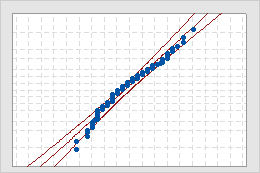
- Middle line
- The expected percentile from the distribution based on maximum likelihood parameter estimates.
- Confidence bound lines
- The left curved line indicates the lower bounds of the confidence intervals for the percentiles. The right curved line indicates the upper bounds of the confidence intervals for the percentiles.
- Anderson-Darling test statistic and p-value
- The results of a test to determine whether your data follow the distribution.
Interpretation
Use the normal probability plots to assess the requirement that your data follow a normal distribution.
If the normal distribution is a good fit for the data, the points form an approximately straight line and fall along the fitted line that is located between the confidence bounds. Departures from this straight line indicate departures from normality. If the p-value is greater than 0.05, you can assume that the data follow the normal distribution. You can evaluate the capability of your process using a normal distribution.
Note
If the distributions differ for multiple variables, you should perform a separate capability analysis for each variable.
Capability Histogram
The capability histogram shows the distribution of your sample data for each variable. Each bar on the histogram represents the frequency of data within an interval.
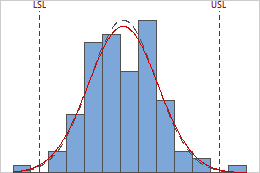 The within and overall curves on the histogram are normal distribution curves that are generated using the process mean and different estimates of process variation. The dashed within curve uses the within-subgroup standard deviation. The solid overall curve uses the overall standard deviation.
The within and overall curves on the histogram are normal distribution curves that are generated using the process mean and different estimates of process variation. The dashed within curve uses the within-subgroup standard deviation. The solid overall curve uses the overall standard deviation. Interpretation
Use the capability histogram to view your sample data in relation to the distribution fit and the specification limits.
- Look for evidence of nonnormality
-
For each variable, compare the solid overall curve to the bars of the histogram to assess whether your data are approximately normal. If the bars vary greatly from the curve, your data may not be normal and the capability analysis results might be inaccurate. If your data appear to be nonnormal, use Individual Distribution Identification to determine whether you should transform the data or fit a nonnormal distribution to perform the capability analysis.
- Compare the within and overall curves
-
For each variable, compare the solid overall curve and the dashed within curve in the histogram to see how closely the curves are aligned. A substantial difference between the curves may indicate that the process is not stable or that there is a significant amount of variation between subgroups for that variable. Use a control chart to assess whether your process is stable for the variable before you perform a capability analysis.
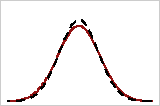
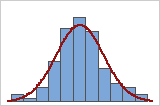
Closely aligned
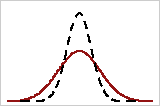
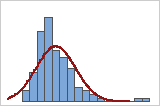
Poorly aligned
- Examine the sample data in relation to the specification limits
- For each variable, visually examine the data in the histogram in relation to the lower and upper specification limits. Ideally, the spread of the data is narrower than the specification spread, and all the data are inside the specification limits. Data that are outside the specification limits represent nonconforming items.
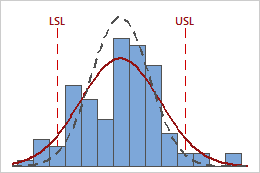
In these results, the process data appear fairly centered between the specification limits. However, the process spread is larger than the specification spread, which suggests poor capability. Although most of the data are within the specification limits, there are nonconforming parts below the lower specification limit (LSL) and above the upper specification limit (USL).
Note
To determine the actual number of nonconforming items in your process, use the results for PPM < LSL, PPM > USL, and PPM Total. For more information, go to All statistics and graphs.
For a more thorough analysis of the assumptions for normal capability analysis, use Normal Capability Sixpack.