Download da macro
Certifique-se de que o Minitab sabe onde encontrar a macro baixada. Selecione . Em Local da macro navegue até o local em que você salva os arquivos de macro.
Importante
Se você usar um navegador mais antigo, quando clicar no botão Download, o arquivo pode abrir no Quicktime, que compartilha a extensão de arquivo .mac com macros do Minitab. Para salvar a macro, clique com o botão direito do mouse no botão Download e selecione Salvar arquivo como.
Entradas obrigatórias
Você precisa de uma coluna de dados de séries temporais.
Entradas opcionais
- AR K…K
- Se você tiver algum parâmetro autorregressivo estimado e quiser executar a verificação de modelo espectral, insira esses parâmetros aqui.
- DIF K
- Se você tiver um componente de diferenciação, insira a ordem de diferenciação aqui.
- MA K…K
- Se você tiver algum parâmetro de média móvel estimada e deseja executar a verificação de modelo espectral, insira esses parâmetros aqui.
- VARIANCE K
- Digite sua variância estimada (padrão = 1,0).
- SMOOTH K
- Informe o tamanho da média móvel (padrão = 3). O tamanho da média móvel deve ser um inteiro ímpar.
- ONEDOC
- Informe se deseja todos os gráficos em uma página.
- SPERIOD C C
- Informe se deseja armazenar as coordenadas para o periodograma. A primeira coluna conterá I (ômega) e a segunda coluna conterá ômega.
- SCUMUL C C C C
- Insira se você deseja armazenar as coordenadas para um periodograma cumulativo. A primeira coluna conterá U(j), a segunda coluna conterá o limite de significância superior, a terceira coluna conterá o limite de significância inferior e a quarta coluna conterá o eixo X.
- SSPEC C C C C
- Informe se deseja armazenar as coordenadas para a estimativa espectral. A primeira coluna conterá a estimativa espectral, a segunda coluna conterá o limite de confiança superior, a terceira coluna conterá o limite de confiança inferior e a quarta coluna conterá ômega.
- SMODEL C C C C
- Informe se você deseja armazenar as coordenadas para a verificação do modelo espectral. A primeira coluna conterá F(ômega), a segunda coluna conterá o limite de confiança superior, a terceira coluna conterá o limite de confiança inferior, a quarta coluna conterá as estimativas espectrais e a quinta coluna conterá ômega.
Execução da macro
Suponha que os dados estejam em C1. Para executar a macro, selecione e digite:
%SPECTRAL C1Clique em Ensaio.
Informações adicionais
Periodograma
O periodograma é uma ferramenta que pode ser utilizada para detectar os componentes cíclicos de uma série temporal. O periodograma é definido da seguinte forma:
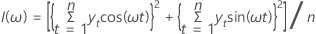
Apesar de o periodograma ser definido para ω = 0, este ponto é excluído porque corresponde à média amostral (que não é de interesse). Se n for ímpar, excluímos ω =π.
Periodograma cumulativo
O periodograma cumulativo é uma aplicação direta do periodograma para testar a hipótese de que uma série temporal específica seja uma sequência de ruído branco. O periodograma cumulativo é uma ferramenta de diagnóstico eficaz para resíduos. O periodograma cumulativo é definido como:
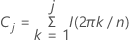
j=1,...,m em que m é o maior inteiro estritamente menor que n/2
Um gráfico de U j contra j /(m −1) é conhecido como periodograma cumulativo.
Também podemos definir valores críticos para testar a hipótese de ruído branco. O nível de significância que a macro usa é de 10% (valor crítico = 1.224). Duas linhas paralelas, com o seguinte intercepto de y definem a região crítica:
Estimativa espectral
A estimativa espectral,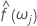 
, pode ser extraída simplesmente tomando-se uma média móvel de ordem 2p + +1 (em que p é um número inteiro positivo) das coordenadas calculadas pelo periodograma. Também é possível definir limites de confiança nessa estimativa espectral:
Os limites de confiança inferiores e superiores podem ser definidos como:
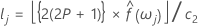
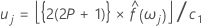
Espectro de um processo ARMA
A estimativa espectral é a estimativa do espectro com base nos dados. O espectro é baseado nos valores reais de população para os parâmetros do modelo. O espectro de um Processo AR (p) pode ser definido como se segue:
O espectro de um processo MA(q) pode ser definido da seguinte forma:
O espectro de um processo ARMA (p, q) (em que p e q são ordens) pode ser definido como se segue:
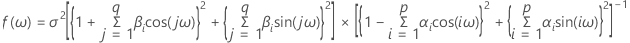
Verificação do modelo espectral para um processo ARIMA
Podemos comparar a estimativa espectral calculada a partir de uma série temporal observada para o espectro verdadeiro com base nos parâmetros do modelo. Intuitivamente, se a estimativa espectral for aproximadamente estatisticamente igual ao verdadeiro espectro, podemos concluir que nossos parâmetros de modelo estimados são adequados na modelagem da série.
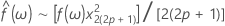
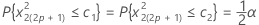
Assim, podemos definir os limites de confiança para determinar se a estimativa espectral está ou não dentro destes limites.
Exemplo 1
Para um exemplo de periodograma, periodograma cumulativo e estimativa espectral, considere o conjunto de dados 'Ciclo 1, fase folicular tardia' (Diggle, p. 228). Para executar a macro, selecione e digite:
%SPECTRAL C1Em primeiro lugar, o periodograma (não mostrado) indica que esta série tem um componente cíclico a ela por causa de seu pico dominante. Às vezes, o eixo X é transformado em uma escala mais significativa, de modo que ele possa ser mais facilmente determinado no ponto do tempo em que o componente cíclico esteja ocorrendo. Por esta razão, a macro tem opções de armazenamento para que o usuário possa transformar o eixo (é possível, então, usar os recursos gráficos no MINITAB para gerar gráficos). Em segundo lugar, os periodogramas cumulativos indicam que esta série não é uma sequência de ruído branco, porque alguns dos pontos de dados vão além dos limites de significância (representados pelas linhas pontilhadas paralelas). Por fim, a estimativa espectral (calculada pela média móvel de três pontos padrão) é apresentada pela linha vermelha, enquanto os limites de confiança são exibidos pelas linhas pontilhadas. Este gráfico nos dá algum vislumbre sobre como deve ser o verdadeiro espectro populacional. Todos os três gráficos correspondem aos gráficos dados em Diggle (p. 52, 55, 106).
Exemplo 2
Para uma análise ARIMA completa, considere o conjunto de dados, 'Ciclo 2, fase folicular tardia' (Diggle, p. 228). Primeiro, calcule o periodograma, o periodograma cumulativo e a estimativa espectral. Eu também colocarei esses três gráficos em uma página usando o subcomando 'Onedoc'. Selecione e digite:
%SPECTRAL C2;
ONEDOC.
Os gráficos (não mostrados) deixam claro que as séries temporais não são uma sequência de ruído branco porque tanto o periodograma como a estimativa espectral indicam séries de frequência baixa dos picos dominantes a valores pequenos de ômega, e o periodograma cumulativo exibe pontos significativos. Portanto, nós vamos usar o MINITAB para modelar esta série temporal com o algoritmo ARIMA. Depois de observar vários modelos, o melhor é um AR(1).
Agora, vamos utilizar a macro para avaliar este modelo empírico. Observe como a estimativa do parâmetro autorregressivo e a estimativa da variância (da saída ARIMA) são inseridos na seguinte linguagem de comando. Selecione e digite:
%SPECTRAL C2;
AR 0.5860;
VARIANCE 0.20603;
ONEDOC.
Os gráficos resultantes simplesmente exibem novamente os gráficos já vistos juntos com a verificação do modelo espectral. No que se refere à verificação do modelo espectral, os círculos vermelhos representam a estimativa espectral, a linha preta sólida é o espectro "verdadeiro" baseado em nossos parâmetros de modelo ARIMA estimado. As linhas pontilhadas representam os limites de confiança do espectro "verdadeiro". Como quase todas as médias móveis de três pontos (círculos vermelhos) estão contidas dentro do intervalo de confiança para o espectro verdadeiro, podemos concluir que o modelo é válido. Por fim, desejamos executar a macro nos resíduos para garantir que eles sejam resíduos de ruído branco. Na verdade, o periodograma cumulativo indica que os resíduos seguem uma sequência de ruído branco.
Referências
Diggle, P. J. Time Series, A Biostatistical Introduction. Oxford: Clarendon Press, 1990.
