Download da macro
Certifique-se de que o Minitab sabe onde encontrar a macro baixada. Selecione . Em Local da macro navegue até o local em que você salva os arquivos de macro.
Importante
Se você usar um navegador mais antigo, quando clicar no botão Download, o arquivo pode abrir no Quicktime, que compartilha a extensão de arquivo .mac com macros do Minitab. Para salvar a macro, clique com o botão direito do mouse no botão Download e selecione Salvar arquivo como.
Entradas obrigatórias
É necessário até cinco matrizes do experimento.
Entradas opcionais
- Tipo do modelo MODEL
- Especifica o modelo a ser testado ao se executar o experimento. O padrão é "interação". É possível inserir vários modelos, como linear, quadrático, interação, quadrático puro. Cada modelo inclui os seguintes termos:
- Linear: constante e termos lineares
- Interação: constante e termos lineares e de produto cruzado
- Quadrático: interação mais termos quadráticos
- Quadrático puro: constante e termos lineares e quadráticos
- RESOLUTION K
- Use para especificar o número de pontos do experimento amostrados usados para estimar a variância de predição mínima, máxima e integrada em cada valor distinto do raio. Para experimentos rotacionáveis você pode selecionar uma pequena resolução. Para experimentos não rotacionáveis pode ser necessário aumentar a resolução conforme o número de fatores aumenta. O padrão é 500 pontos de experimento.
- INCREMENT K
- Use para especificar o incremento do raio. Você pode mudar este valor para exibir o gráfico com uma resolução maior ou menor. O valor padrão é 0.1 unidades codificadas.
- MAXDIST K
- Indica a distância máxima do raio. Por padrão, isto é definido como a maior distância ao ponto do experimento que está mais distante do centro do experimento. Para um VDG que está baseado em múltiplos experimentos, o MAXDIST é definido como a maior distância de todos os experimentos.
Execução da macro
Suponha que os fatores de um CCD foram copiados para uma matriz M1 e os fatores para um experimento Box-Behnken foram armazenados em M2. Para executar a macro, selecione e digite:
%VDG M1 M2;
MODEL "quadratic";
RESOLUTION 150.Clique em Ensaio.
Mais informações
Gráficos de Dispersão de Variância e Desenho de Experimentos
Os gráficos de dispersão de variância são ferramentas gráficas usadas no processo de seleção de um planejamento de experimentos (DOE). Esses gráficos mostram a variância da predição escalada de um DOE em todo o espaço do experimento e são tipicamente usados para comparar experimentos de superfície de resposta. Contudo, os gráficos de dispersão de variância também podem ser usados para comparar o desempenho de múltiplos experimentos para um modelo específico, como um modelo linear, um modelo linear com termos de interação, um modelo linear com termos quadráticos ou um modelo totalmente quadrático.
Histórico e Fundamentos de VDG
O VDG foi desenvolvido originalmente por Giovannitti-Jensen e Myers (1989) e Myers et al. (1992) para exibir um instantâneo da estabilidade da variância da predição escalada em todo o espaço do experimento.
Matematicamente, a variância de predição escalada pode ser estimada com a equação abaixo:
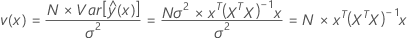
onde v(x) é a variância de predição escalada no ponto x e, conforme mostrado acima, não depende dos dados de resposta, apenas na matriz do experimento X. Em outras palavras, a variância de predição escalada é uma função do número de ensaios em seu experimento, a matriz de covariância, e o ponto no qual você estiver avaliando a variância de predição. Como a variância de predição de escala exibida pelo VDG é independente dos dados de resposta, o VDG permite avaliar a qualidade de um experimento pela causa.
Em geral, um VDG é construído com quatro componentes básicos:
- · Um gráfico da variância esférica em relação ao raio r. A média da variância esférica é v(x) medida (integrada) na superfície de um esfera de raio r.
- · Um gráfico da variância de predição máxima em um raio r para múltiplos valores de r começando pela origem (r começa em zero e sofre pequenos incrementos até atingir o ponto no experimento mais longe da origem).
- · Um gráfico da variância de predição mínima em um raio r para múltiplos valores de r começando pela origem.
- · Uma linha horizontal em v(x) = p, onde p é o número de parâmetros no modelo a ser ajustado. Um experimento "ótimo" faria com que a variância de predição máxima fosse menor que ou igual a p para todos os pontos no espaço do experimento.
O VDG mostra a variância de predição escalada média, máxima e mínima para diferentes valores de r, que representa a distância de qualquer ponto até a origem ou o centro do experimento.
Uso de VDG para avaliar outros aspectos de um experimento
Usando um VDG, é possível avaliar o desempenho de um experimento único em termos de sua variância de predição. Também é possível usar o VDG para comparar dois ou mais experimentos. Outra aplicação de um VDG é avaliar o efeito da adição de pontos centrais em um experimento.
Você também pode usar um VDG para avaliar se um experimento e rotacionável. Em um experimento rotacionável, todas as três linhas (mínima, média e máxima) no gráfico irão coincidir. Se as linhas mínima, média e máxima não coincidirem, o experimento de face centrada não é rotacionável.
Simulação de Monte Carlo para estimar variância de predição
Esta seção avançada descreve os métodos matemáticos usados para estimar as variâncias de predição mínima, máxima e média exibidas em um VDG. Se você estiver interessado apenas em como executar uma macro para exibir e interpretar um VDG, pule esta seção.
Como mencionado anteriormente, para um valor fixo do raio, é preciso realizar uma pesquisa para encontrar as variâncias de predição escalada mínima, máxima e integrada. O método selecionado para a macro do Minitab está baseado na simulação de Monte Carlo e na habilidade para pesquisar uniformemente em pontos equidistantes do centro x = (0,0,…,0)T do experimento.
Três quantidades precisam ser calculadas em distâncias diferentes da origem: 1) a variância de predição mínima, 2) a variância de predição máxima e 3) a variância de predição integrada. Há múltiplas maneiras de encontrar essas quantidades. Um método é através do uso de um algoritmo de programação não-linear para encontrar as variâncias de predição mínima e máxima. Contudo, o método que escolhemos para estimar essas quantidades é através da amostragem uniforme e do encontro de um grande conjunto de pontos distintos que são a mesma distância do centro do experimento para diferentes valores de r. Do espaço de pontos equidistantes, pode-se garantir a estimativa adequada das variâncias de predição mínima e máxima tendo duas condições satisfeitas: primeiro, a amostragem de pontos equidistantes precisa ser uniforme. Em outras palavras, não pode haver regiões onde alguns pontos equidistantes têm maior probabilidade de serem escolhidos do que outros. Em segundo lugar, o número de pontos precisa ser grande o suficiente para cobrir todo o espaço de possíveis pontos do experimento.
Como todos os pontos que devem ser amostrados são equidistantes, o problema de amostragem equivale a encontrar uma boa maneira de obter pontos de uma bola n ou hiperesfera para um determinado raio.
O procedimento está descrito em Marsaglia (1972) e é resumido abaixo:
- Gere um vetor n-dimensional de variáveis aleatórias normais (por ex. de uma distribuição normal padrão). Permita que este vetor seja x = (x1, x2,…,xn). Crie múltiplos vetores x.
- Calcule o raio p para todos os pontos x que você gerou.

- Transforme cada um dos pontos originais do experimento obtidos no passo 1 multiplicando-se cada entrada do vetor x por r, onde r representa o raio da hiperesfera da qual a amostra é obtida.
Nós ilustramos como amostrar pontos em uma hiperesfera de raio r constante. Podemos usar esta técnica de amostragem para estimar a variância de predição máxima ou mínima. Usando essas amostras, da Fraca Lei dos Grandes Números, a variância de predição média dos pontos de experimentos amostrados pode ser usada para estimar a verdadeira variância de predição integrada contanto que n seja grande.
Referências
[1] Marsaglia G. "Choosing a Point from the Surface of a Sphere". The Annals of Mathematical Statistics, Vol. 43, No. 2 (1972), pp. 645-646.
[2] Myers R, Montgomery D. (2002). Response Surface Methodology - Process and Product Optimization Using Designed Experiments, Second Edition. John Wiley & Sons, Inc.
