Download da macro
Certifique-se de que o Minitab sabe onde encontrar a macro baixada. Selecione . Em Local da macro navegue até o local em que você salva os arquivos de macro.
Importante
Se você usar um navegador mais antigo, quando clicar no botão Download, o arquivo pode abrir no Quicktime, que compartilha a extensão de arquivo .mac com macros do Minitab. Para salvar a macro, clique com o botão direito do mouse no botão Download e selecione Salvar arquivo como.
Entradas obrigatórias
- Uma coluna de dados de resposta numéricos
- Uma coluna correspondente de níveis de fator
Observação
Você pode usar os dados não empilhados, especificando o subcomando UNSTACKED.
Entradas opcionais
- UNSTACKED
- Especifique se os dados estão desempilhados.
- FALPHA
- Use para especificar o nível alfa da família desejada (o padrão é 0,20).
- CONTROL C
- Use para especificar a coluna (C) para ser o controle.
Observação
Se os dados estiverem empilhados, a resposta para o grupo de controle não deve estar na mesma coluna que a resposta para os outros níveis de fator. A resposta para o grupo de controle deve estar em uma coluna separada.
Execução da macro
Suponha que os dados de resposta estejam em C1 e os níveis de fator estejam em C2. Para executar a macro, selecione e digite o seguinte:
%KRUSMC C1 C2Clique em Ensaio.
Saída
A primeira parte da saída será exibida no número de comparações (k) que está sendo feito,
, a família alfa (α), o alfa individual de Bonferroni (β), 
, e o valor z crítico bilateral.
A próxima seção exibe nossas diferenças de posto médio de grupo padronizado (θ) e os valores-p associados a essas diferenças. Observe que essas tabelas são simétricas, portanto, há asteriscos na parte triangular superior da tabela. Além disso, há zeros abaixo da diagonal da tabela porque a diagonal representa uma comparação entre um grupo e ele mesmo (essas comparações são insignificantes e não são consideradas na análise). Um exemplo de como ler essa tabela é o seguinte: Qual é a diferença entre os grupos 2 e 4? A terceira seção exibe um sinal de intervalos de confiança para as medianas. Os níveis de confiança desses intervalos são controlados no alfa da sua família. Uma vez que esses intervalos são controlados em um alfa geral da família, podemos comparar esses intervalos pareados (Apêndice 2). É importante lembrar que a confiança desejada pode não ser alcançada para todos ou alguns dos intervalos. Além disso, essa cobertura "geral" pelo alfa da família não é exata quando os tamanhos amostrais são diferentes, mas é frequentemente uma aproximação razoável.
A seção final nos mostra o que são nossas diferenças "significativas" (se houver alguma). Nesta seção eu apresento o valor z, o valor z crítico e o valor-p associado ao valor z.
O gráfico exibe as diferenças de padronizadas de posto médio de grupo não-absoluto. Este gráfico também é extremamente útil porque podemos ver não apenas a magnitude das diferenças do grupo, mas a direção também. Ele também exibe os valores z críticos positivos e negativos, de forma que você pode ver se uma diferença é "significativa".
Empate nos dados
Se houver empates nos dados, uma constante não viciada (ou fator de correção) de 2 é calculado. A estatística H é ajustada para 3. O desvio padrão (ξ) também é ajustado por este fator de correção 4. A saída mostrará as tabelas ajustadas e não-ajustadas. Contudo, eu só fornecerei os valores-p para as tabelas ajustadas porque elas são tabelas que devem ser usadas. O motivo principal para exibição das tabelas não-ajustadas é mostrar o que os efeitos dos empates tiveram nos valores z. Se os empates forem extremamente extensos, a validade dos dados deve ser questionada porque esses testes supõem que as distribuições são contínuas. Frequentemente, os empates terão pouco ou nenhum impacto em suas conclusões.
Agradecimentos
Agradecemos ao Dr. Tom Hettmansperger (da Universidade Estadual da Pensilvânia) por sua revisão desta macro, às nossas numerosas discussões relativas a este trabalho e pelo tempo que ele dispensou a tudo isso e à sua paciência. Também agradecemos ao Sr. Nicholas Bolgiano e Sr. Mike Delozier (Minitab, Inc.) por suas sugestões e críticas relacionadas à macro.
Informações adicionais
Teste de Dunn
Uma maneira eficiente de fazer inferência simultânea pareada foi introduzida por Dunn (1964). Primeiro, combinamos os dados, determinamos os postos, encontramos os postos médios de grupo e, depois, obtivemos as diferenças absolutas padronizadas desses postos médios.
Seja k = o número de tratamentos, 
Seja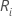 
= à soma das posições para o iésimo tratamento, i = 1,…,k
Seja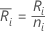 
Em que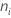 
= o número de observações para o iésimo tratamento
Seja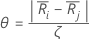 
Em que j=l,...,k e j 
i
Em que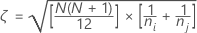 
Estatística H
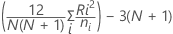
Em que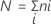 
Declararemos, então, se a "significância":
Em que 
Em que α é um valor alfa da família especificado, 
