Um engenheiro de qualidade de uma fábrica de motores deseja realizar um teste de bimodalidade em pistões de dois fornecedores. O engenheiro mede o comprimento de uma amostra aleatória de 100 pistões de cada um dos fornecedores.
O script usa o pacote diptest para R para testar se os dados são unimodais. Se o teste rejeitar a hipótese nula para dados unimodais, o script pressupõe que os dados são uma combinação de duas distribuições normais. O script usa o pacote mixtools para R para exibir estatísticas descritivas e curvas de densidade para duas distribuições normais.
- Passe uma única coluna de uma worksheet do Minitab como entrada.
- Adicione um título de tabela.
- Adicionar rótulos de coluna para uma tabela.
- Envie uma tabela para o painel Saída do Minitab.
- Crie um gráfico e envie-o para o painel Saída do Minitab.
| Arquivo | Descrição |
|---|---|
| bimodal.R | Um R script que pega uma coluna de uma planilha do Minitab, testa a unimodalidade e produz resultados para uma combinação de duas distribuições normais se os dados não forem unimodais. |
Todos os arquivos mencionados neste guia estão disponíveis neste arquivo .ZIP : r_guide_files.zip.
Pré-requisitos
-
O script R no exemplo abaixo requer os seguintes pacotes R:
- mtbr
- O pacote R que integra o Minitab e o R. No exemplo, as funções deste módulo enviam resultados do R para o Minitab. Para obter informações sobre como instalar o pacote do R Minitab, vá para a Etapa 2: Instale o mtbr.
- mixtools
- O R pacote que o script usa para criar saída para uma mistura de distribuições normais.
- diptest
- O R pacote que o script usa para testar se os dados são unimodais.
install.packages("mixtools")Para obter ajuda com a instalação de pacotes, consulte o departamento de R suporte técnico da sua organização. O Suporte Técnico do Minitab não pode ajudar na instalação de R pacotes.
Etapas para executar o exemplo
- Instale os módulos necessários: mtbr.
- Salve o arquivo de script do R, bimodal.R, no local do arquivo padrão do Minitab. Para obter mais informações sobre onde o Minitab procura os arquivos de script do R, acesse Pastas padrão de arquivos R para o Minitab.
- Abra o conjunto de dados de amostra Custodeenergiadeprocesso.MWX.
-
No painel Linha de
comando do Minitab, digite
RSCR "bimodal.R" "Process 1". - Selecione Ensaio.
bimodal.R
# Load the necessary libraries
#Original code by Valentina Tillman
library(mixtools)
library(mtbr)
library(diptest)
# Retrieve sample data
input_column <- commandArgs(trailingOnly = TRUE)
data <- mtb_get_column(input_column)
dip_test_result <- dip.test(data)
if (dip_test_result$p.value < 0.05) {
# Fit a bimodal mixture model
bimodal_fit <- normalmixEM(data, k = 2)
# Manually extract parameter estimates and format them as a data frame
bimodal_table <- data.frame(
Mean = bimodal_fit$mu,
Standard_Deviation = bimodal_fit$sigma,
Proportion = bimodal_fit$lambda #tells you what % of the data is clustered around which mean. Also called lambda
)
# Define title and headers
mytitle <- "Modeling a Bimodal Distribution"
myheaders <- names(bimodal_table)
# Add the table to the mtbr output
mtb_add_table(columns = bimodal_table, headers = myheaders, title = mytitle)
png("r_bimodal_image.png")
plot(bimodal_fit, density = TRUE, which = 2)
graphics.off()
mtb_add_image("r_bimodal_image.png")
# Now generate tolerance intervals using the parameters found using mixtools
# Set the desired coverage level (e.g., 95%)
coverage_level <- 0.95
alpha <- 1 - coverage_level
# Calculate the tolerance intervals for each component
tolerance_intervals <- lapply(1:2, function(i) {
mu <- bimodal_fit$mu[i]
sigma <- bimodal_fit$sigma[i]
n <- bimodal_fit$lambda[i] # proportion of the component
# Calculate the critical value for the normal distribution
z <- qnorm(1 - alpha / (2 * n))
# Calculate lower and upper bounds of the tolerance interval
lower_bound <- mu - z * sigma
upper_bound <- mu + z * sigma
c(lower_bound, upper_bound)
})
# Show the tolerance intervals
tolerance_intervals_df <- data.frame(
Component = c("First Mode", "Second Mode"),
Lower_Bound = sapply(tolerance_intervals, "[", 1),
Upper_Bound = sapply(tolerance_intervals, "[", 2)
)
myheaders <- c("Component", "Lower Bound", "Upper Bound")
mytitle <- "Tolerance Intervals for Bimodal Distribution"
mtb_add_table(columns = tolerance_intervals_df, headers = myheaders, title = mytitle)
} else {
mtb_add_message("This data is unimodal.")
}
Resultados
Modeling a Bimodal Distribution
| Mean | Standard_Deviation | Proportion |
|---|---|---|
| 34.1875 | 1.50909 | 0.516129 |
| 48.3333 | 1.84992 | 0.483871 |
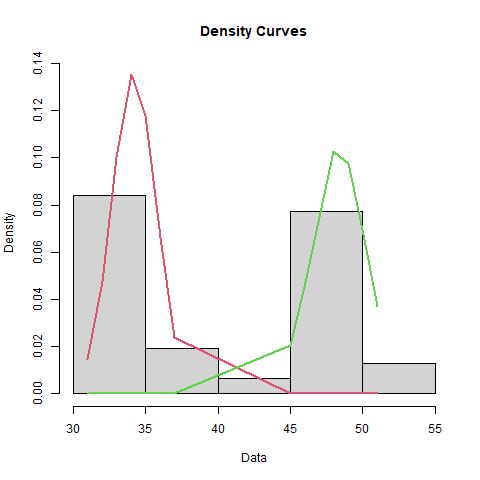
Tolerance Intervals for Bimodal Distribution
| Component | Lower Bound | Upper Bound |
|---|---|---|
| First Mode | 31.6821 | 36.6929 |
| Second Mode | 45.3200 | 51.3467 |
