Teste exato de Fisher
O teste exato de Fisher é um teste de independência. O teste é baseado em uma distribuição exata, e não em uma distribuição aproximada do qui-quadrado que é utilizada para o teste de Pearson e da razão de verossimilhança. O teste exato de Fisher é útil quando as contagens de células esperadas são baixas e a aproximação do qui-quadrado não é muito boa.
Fórmula
- tamanho da população
- número total de observações
- número de sucessos na população
- número de observações na primeira linha
- Tamanho amostral
- número de observações na primeira coluna
Exemplo
| Criança | Adulto | Linha Total | |
|---|---|---|---|
| Açúcar | 9 | 1 | 10 |
| Pedaços de chocolate | 2 | 8 | 10 |
| Coluna Total | 11 | 9 | 20 |
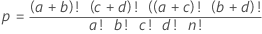
| Criança | Adulto | Linha Total | |
|---|---|---|---|
| Açúcar | a | b | a+b |
| Pedaços de chocolate | c | d | c+d |
| Coluna Total | a+c | b+d | a+b+c+d |
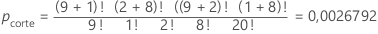
Para este exemplo, a soma dos valores-p inferiores ou iguais a pcorte para as outras matrizes possíveis é de 0,0054775.
Teste exato de McNemar
O teste de McNemar compara as proporções que são observadas antes e depois de um tratamento. Por exemplo, é possível usar o teste de McNemar para determinar se um programa de treinamento altera a proporção de participantes que respondem corretamente a uma pergunta.
As observações para o teste de McNemar podem ser resumidas em uma tabela de dois por dois, como mostrado abaixo.
| Depois do tratamento | |||
| Antes do tratamento | Condição verdadeira | Condição não verdadeira | Total |
| Condição verdadeira | n11 | n12 | n1. |
| Condição não verdadeira | n21 | n22 | n2. |
| Total | n·1 | n·2 | n·· |
A condição para o exemplo de treinamento é uma resposta correta. Portanto, n21 representa o número de participantes que responderam corretamente a pergunta após o treinamento, mas não antes dele. E n12 representa o número de participantes que responderam corretamente a pergunta antes do treinamento, mas não depois dele. O número total de participantes é representado por n...
Diferença estimada
Seja δ a diferença entre as probabilidades marginais, p1.- p.1, na população. A diferença estimada,  , é dada pela seguinte fórmula:
, é dada pela seguinte fórmula:
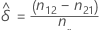
Intervalo de confiança
Um intervalo de confiança aproximado de 100(1 – α)% é dado pela seguinte fórmula:

em que α é o nível de significância para o teste, z α/2 é o escore Z associado a uma probabilidade de cauda de α/2, e EP é dado pela seguinte fórmula:
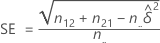
Valor-p
A hipótese nula é δ = 0. O valor-p exato para o teste da hipótese nula é calculado da seguinte maneira:

em que X é uma variável aleatória que é extraída a partir de uma distribuição binomial com uma probabilidade de eventos de 0,5 e um número de ensaios iguais a n21 + n12.
O teste Mantel-Haenszel-Cochran
O teste pressupõe que não existe interação de 3 fatores. O objetivo do teste consiste em avaliar o grau de relacionamento entre as duas variáveis dicotômicas ao controlar para uma variável de perturbação. A estatística de MHC é comparada com um percentil de qui-quadrado com um grau de liberdade.
O teste Mantel-Haenszel-Cochran (MHC) se aplica somente se existirem três ou mais variáveis de classificação, e as duas primeiras variáveis tiverem dois níveis cada. Todas as variáveis além das duas primeiras são tratadas como uma única variável Z para as finalidades do teste MHC, com cada combinação de níveis tratada como um nível de Z.
Fórmula
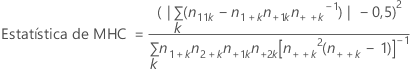
Notação
| Termo | Descrição |
|---|---|
| k | Nível de Z |
| n11k | número de observações na primeira linha, primeira coluna |
| n1+k | número de observações na primeira linha |
| n+1k | número de observações na primeira coluna |
| n++k | número de observações total |
| n2+k | número de observações na segunda linha |
| n+2k | número de observações na segunda coluna |
