Neste tópico
Número de pares concordantes e discordantes
Um par é concordante se o posto da observação mais elevada na variável X também for o posto mais elevado na variável Y. O par é discordante se o posto mais elevada da observação em X ocupa o posto mais baixo em Y. O par está empatado se os indivíduos apresentarem a mesma classificação de X e/ou Y.
Fórmula


Notação
| Termo | Descrição |
|---|---|
| nij | observações na célula correspondente à ia linha e ja coluna |
Gama
O gama de Goodman e Kruskal é uma medida de associação entre as variáveis ordinais. Existe uma associação perfeita, então |γ| = 1. Se X e Y são independentes, Y = 0.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares concordantes = Σi<kΣj>l nij nkl |
| nij | observações na célula correspondente à ia linha e ja coluna |
D de Somers
O D de Somers mede a força e a direção da relação entre duas variáveis ordinais.
Fórmula
Com Y como variável de resposta:

Com X como variável de resposta:

Notação
| Termo | Descrição |
|---|---|
| TX | número de pares empatados em X = 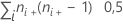 |
| TY | número de pares empatados em Y = 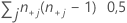 |
| C | número de pares concordantes |
| D | número de pares discordantes |
| ni+ | número de observações na ia linha |
| n+j | número de observações na ja coluna |
| nij | observações na célula correspondente à ia linha e ja coluna |
| n++ | número de observações total |
Tau-b de Kendall
O tau-b de Kendall, como o gama, mede a associação entre variáveis ordinais. Um dos pontos fortes de de tau-b de Kendall como uma medida da associação é que ele é responsável por pares empatados no cálculo. O gama apresenta um problema com pares empatados, de modo que gama mostra quase sempre uma associação maior do que tau-b. Os valores de tau-b variam entre -1,0 e 1,0.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| TX | número de pares empatados em X = Σi ni+ (ni+- 1) 0,5 |
| TY | número de pares empatados em Y = Σj n+j (n+j- 1) 0,5 |
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares concordantes = Σi<kΣj>l nij nkl |
| ni+ | número de observações na ia linha |
| n+j | número de observações na ja coluna |
| nij | observações na célula correspondente à ia linha e ja coluna |
| n++ | número de observações total |
Teste de concordância
O teste de concordância é um teste de independência. O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.
Fórmula
O teste de concordância utiliza uma estatística padrão de teste normal:

O valor de p é igual à probabilidade de que Z seja maior que Z*.
Notação
| Termo | Descrição |
|---|---|
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares discordantes = Σi<kΣj>l nij nkl |
| SE(C-D) | Erro padrão ou C-D, que é aproximadamente igual a 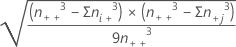 |
| n++ | o número de observações total |
| ni+ | o número de observações na i-ésima linha. |
| n+j | o número de observações na j-ésima coluna. |
