Interpretar os principais resultados para Teste qui-quadrado de qualidade de ajuste

Conclua as etapas a seguir para interpretar um teste da qualidade do ajuste para o qui-quadrado. A saída principal inclui o valor-p e um gráfico de barras dos valores esperados e observados.

Neste tópico

Etapa 1. Determine se os valores observados são estatisticamente diferentes dos valores esperados
Etapa 2: Examine a diferença entre os valores observados e esperados para cada categoria

Etapa 1. Determine se os valores observados são estatisticamente diferentes dos valores esperados

Use o valor-p para determinar se deve rejeitar ou não a hipótese nula, o que indica que as proporções da população em cada categoria são consistentes com os valores especificados em cada categoria.

Para determinar se os valores observados da amostra e os valores esperados da distribuição especificada são estatisticamente diferentes, compare o valor-p com o nível de significância. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de rejeitar incorretamente a hipótese nula.

Valor-p ≤ α: os dados observados são estatisticamente diferentes dos valores esperados (rejeitar H₀): Se o valor-p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os dados não seguem a distribuição com determinadas proporções. Use seu conhecimento especializado para determinar se a diferença é praticamente significativa.
Valor-p > α: não é possível concluir que os dados observados sejam estatisticamente diferentes dos valores esperados (não deve rejeitar H₀): Se o valor-p for maior do que o nível de significância, você não deve rejeitar a hipótese nula porque não há evidências suficientes para concluir que os dados não seguem uma distribuição com as proporções especificadas. No entanto, não é possível concluir que as distribuições são as mesmas. A diferença pode existir, mas o teste pode não ter poder suficiente para detectá-la.

Teste qui-quadrado

N	GL	Qui-Quadrado	Valor-p
225	3	0,648148	0,885

Resultados principais: valor-p

Nestes resultados, o valor-p é 0,885. Como o valor-p é maior do que o valor α escolhido de 0,05, você não deve rejeitar a hipótese nula. Portanto, não é possível concluir que as proporções observadas são significativamente diferentes das proporções especificadas.

Etapa 2: Examine a diferença entre os valores observados e esperados para cada categoria

Use o gráfico de barras que representa graficamente cada os valores observados e esperados de cada categoria para determinar se há uma diferença em uma categoria específica.

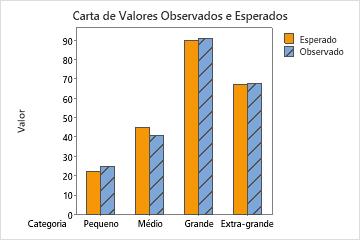
Este gráfico de barras indica que os valores observados são muito semelhantes aos valores esperados para cada categoria. Assim, o gráfico de barras confirma visualmente o que o valor-p indica — que não é possível concluir que as proporções observadas são significativamente diferentes das proporções especificadas.