Interpretar todas as estatísticas e gráficos para Teste qui-quadrado de qualidade de ajuste

Encontre definições e orientações interpretação para cada estatística e gráfico fornecido com o teste de qualidade de ajuste para qui-quadrado.

Neste tópico

Gráfico de contribuição para o valor de qui-quadrado
Gráfico de valores observados e esperados
Qui-quadrado e contribuição ao Qui-Quadrado
DF

N
Valores observados e esperados
Valor-p

Gráfico de contribuição para o valor de qui-quadrado

Este gráfico de barras representa graficamente a contribuição de cada categoria para a estatística qui-quadrado global. Você pode escolher um gráfico que ordene as categorias por contribuição, desde a maior contribuição até a menor contribuição.

Interpretação

Categorias com uma grande diferença entre os valores observados e esperados fazem uma contribuição maior para a estatística qui-quadrado global.

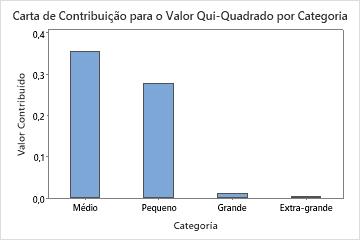
Este gráfico de barras indica que a maior contribuição para a estatística qui-quadrado está na categoria Média.

Gráfico de valores observados e esperados

Use o gráfico de barras que representa graficamente cada os valores observados e esperados de cada categoria para determinar se há uma diferença em uma categoria específica.

Se você determinou que a diferença entre as contagens observadas e esperadas é estatisticamente significativa, você pode usar este gráfico de barras para determinar quais categorias apresentam a maior diferença entre os valores observados e esperados.

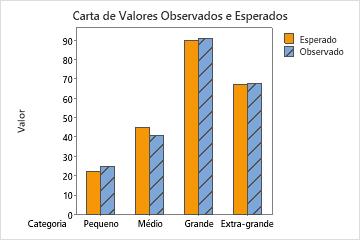
Este gráfico de barras indica que os valores observados são muito semelhantes aos valores esperados para cada categoria. Assim, o gráfico de barras confirma visualmente o que o valor-p indica — que não é possível concluir que as proporções observadas são significativamente diferentes das proporções especificadas.

Qui-quadrado e contribuição ao Qui-Quadrado

Use a categoria de contribuições individuais para estabelecer o quanto do total da estatística qui-quadrado é atribuível a cada diferença de categoria entre os valores observados e esperados.

O Minitab calcula a contribuição de cada categoria para a estatística qui-quadrado como o quadrado da diferença entre os valores observados e esperados para uma categoria, dividido pelo valor esperado para essa categoria. A estatística qui-quadrado é a soma destes valores para todas as categorias.

Interpretação

Categorias com uma grande diferença entre os valores observados e esperados fazem uma contribuição maior para a estatística qui-quadrado global.

Nestes resultados, os valores de contribuição de cada categoria somam-se à estatística qui-quadrado geral, que é 0,648. A maior contribuição vem de camisas de tamanho Médio e a menor contribuição vem da categoria Extra Grande.

DF

Os graus de liberdade para o teste da qualidade do ajuste para o qui-quadrado é o número de categorias menos 1.

Interpretação

O Minitab usa os graus de liberdade para determinar o valor-p. Quanto mais categorias que você tem em seu estudo, mais graus de liberdade que você tem.

Nestes resultados, os graus de liberdade (DF) são três.

Teste qui-quadrado

N	GL	Qui-Quadrado	Valor-p
225	3	0,648148	0,885

N

N é o tamanho amostral total. N é igual à soma de todas as contagens observadas.

Interpretação

Nestes resultados, o tamanho amostral total (N) é 225.

Contagens Observadas e Esperadas

Categoria	Observado	Teste de Proporção	Esperado	Contribuição para Qui-Quadrado
Pequeno	25	0,1	22,5	0,277778
Médio	41	0,2	45,0	0,355556
Grande	91	0,4	90,0	0,011111
Extra-grande	68	0,3	67,5	0,003704

Teste qui-quadrado

N	GL	Qui-Quadrado	Valor-p
225	3	0,648148	0,885

Valores observados e esperados

Os valores observados são o número real de observações em uma amostra de que pertencem a uma categoria.

Os valores esperados são o número de observações cuja ocorrência seria esperada, em média, se as proporções de teste fossem verdadeiras. O Minitab calcula as contagens esperadas multiplicando-se as proporções de teste de cada categoria pelo tamanho amostral total.

Interpretação

É possível comparar os valores observados e os valores esperados usando-se a tabela de saída ou o gráfico de barras.

Nestes resultados, as contagens esperadas parecem muito próximas às contagens observadas para todas as categorias.

Valor-p

O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.

Use o valor-p para determinar se deve rejeitar ou não a hipótese nula, o que indica que as proporções da população em cada categoria são consistentes com os valores especificados em cada categoria.

Interpretação

Para determinar se os valores observados da amostra e os valores esperados da distribuição especificada são estatisticamente diferentes, compare o valor-p com o nível de significância. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de rejeitar incorretamente a hipótese nula.

Valor-p ≤ α: os dados observados são estatisticamente diferentes dos valores esperados (rejeitar H₀): Se o valor-p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os dados não seguem a distribuição com determinadas proporções. Use seu conhecimento especializado para determinar se a diferença é praticamente significativa.
Valor-p > α: não é possível concluir que os dados observados sejam estatisticamente diferentes dos valores esperados (não deve rejeitar H₀): Se o valor-p for maior do que o nível de significância, você não deve rejeitar a hipótese nula porque não há evidências suficientes para concluir que os dados não seguem uma distribuição com as proporções especificadas. No entanto, não é possível concluir que as distribuições são as mesmas. A diferença pode existir, mas o teste pode não ter poder suficiente para detectá-la.

Nestes resultados, o valor-p é 0,885. Como o valor-p é maior do que o valor α escolhido de 0,05, você não deve rejeitar a hipótese nula. Portanto, não é possível concluir que as proporções observadas são significativamente diferentes das proporções especificadas.

Teste qui-quadrado

N	GL	Qui-Quadrado	Valor-p
225	3	0,648148	0,885