Neste tópico
Média (Normal)
O desvio padrão é conhecido
O intervalo de confiança para uma média de uma distribuição normal, quando o desvio padrão da população é conhecido é:

A margem de erro é 
Para resolver para n:

O desvio padrão não é conhecido
O intervalo de confiança para uma média de uma distribuição normal quando o desvio padrão da população é desconhecido é:
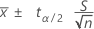
A margem de erro é 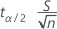
Para resolver para n, calcule o mínimo de n de forma que:
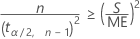
Notação
| Termo | Descrição |
|---|---|
 | média da amostra |
| zα/2 | a probabilidade acumulada inversa da distribuição normal padrão em 1- α /2; α = 1 - nível de confiança/100 |
| σ | population standard deviation (assumed known) |
| n | tamanho médio |
| ME | margin of error |
| t α/2 | a probabilidade acumulada inversa de uma distribuição t com n-1 graus de liberdade a 1-α/2 |
| S | valor de planejamento |
Proporção (Binomial)
Limite inferior
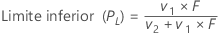
Limite superior

O intervalo (PL, PU) é um intervalo de confiança com aproximadamente 100(1 – α)% de p.
Observação
Para resolver para n, calcule o mínimo de n de forma que:
Notação
| Termo | Descrição |
|---|---|
| v1 (limite inferior) | 2x |
| v2 (limite inferior) | 2(n – x + 1) |
| v1 (limite superior) | 2(x + 1) |
| v2 (limite superior) | 2(n – x) |
| x | número de eventos |
| n | número de ensaios |
| F (limite inferior) | ponto α/2 inferior da distribuição F com v1 e v2 graus de liberdade |
| F (limite superior) | ponto α/2 superior da distribuição F com v1 e v2 graus de liberdade |
Taxa e Média (Poisson)
Fórmula
O limite de confiança de um limite inferior para uma taxa ou média de uma distribuição de Poisson é:
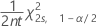
O limite de confiança de um limite superior para uma taxa ou média de uma distribuição de Poisson é:
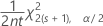
A margem de erro inferior é igual a -1 × (limite de confiança de um limite inferior). A margem de erro superior é igual ao limite de confiança de um limite superior.
Para resolver para n, calcule o mínimo de n de forma que:
(S – SL) ≤ ME and (SU – S) ≤ ME
Notação
| Termo | Descrição |
|---|---|
| n | tamanho amostral |
| t | comprimento de observação; para a média de Poisson, comprimento = 1 |
| s | número total de ocorrências de um processo de Poisson |
| χ2p, x | ponto do percentil de x superior de uma distribuição de qui-quadrado com p graus de liberdade, onde 0 < x < 1 |
| S | valor de planejamento |
| ME | margem de erro |
Variância e desvio padrão (Normal)
Fórmula
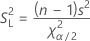
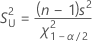
Para obter o intervalo de confiança para o desvio padrão, extraia a raiz quadrada das equações acima.
A margem de erro inferior é igual a -1 × (limite de confiança de um limite inferior). A margem de erro superior é igual ao limite de confiança de um limite superior .
Para resolver para n para variância, calcule o mínimo de n de forma que:
(S2 – S2L) ≤ ME and (S2U – S2) ≤ ME
Para resolver para n para desvio padrão, calcule o mínimo de n de forma que:
(S – SL) ≤ ME and (SU – S) ≤ ME
Notação
| Termo | Descrição |
|---|---|
| n | tamanho médio |
| s2 | variância da amostra |
| Χ2 p | 100po ponto do percentil superior em uma distribuição de qui-quadrado com (n – 1) graus de liberdade |
| S | valor de planejamento |
| ME | margem de erro |
