Etapa 1: Examine os valores calculados
Usando os valores de duas variáveis de função de poder que você inseriu, o Minitab calcula o número de réplicas, o valor máximo da diferença entre as médias de efeito principal ou o poder do experimento.
- Os valores da diferença máxima entre as médias de efeito principal
- A diferença máxima é a diferença que você deseja detectar entre os níveis de fatores que têm as médias mais altas e mais baixas. Os cálculos usam o fator que tem a maioria dos níveis para produzir os cálculos que são conservadores para outros fatores. O Minitab calcula a menor diferença de que o experimento detecta. Mais réplicas dão ao experimento a capacidade de detectar diferenças menores. Normalmente, você quer ser capaz de detectar a menor diferença que tem consequências práticas para a sua aplicação.
- Réplicas
- Se você inserir o valor da diferença máxima entre as médias de efeito principais e o valor de poder, o Minitab calcula o número de réplicas. Réplicas são vários ensaios experimentais com as mesmas configurações de fatores. Como o número de réplicas é um valor inteiro, o poder real pode ser um pouco maior do que seu valor alvo.
- Ensaios totais
- Para cada caso, o Minitab calcula o total de ensaios a partir do número de réplicas. O número de ensaios de uma única réplica é o produto do número de níveis. O número total de ensaios é o produto deste tamanho de experimento de base e o número de réplicas.
- Valores de poder
- Se você inserir o número de réplicas e a diferença máxima entre as médias de efeito principais, o Minitab calcula o valor de poder. O poder é a probabilidade de que você encontre corretamente uma diferença significativa. Em geral, um valor de poder de 0,9 é considerado suficiente. Um valor de 0,9 indica que você tem uma probabilidade de 90% de detectar a diferença entre as configurações de fatores. Mantendo constantes as outras as propriedades do experimento, quando o número total de ensaios é menor ou o máximo é menor, o experimento tem menos poder.
Resultados
| Diferença Máxima | Reps | Total de Ensaios | Poder Alvo | Poder Real |
|---|---|---|---|---|
| 2,0 | 3 | 108 | 0,8 | 0,932615 |
| 2,0 | 3 | 108 | 0,9 | 0,932615 |
| 1,8 | 3 | 108 | 0,8 | 0,867493 |
| 1,8 | 4 | 144 | 0,9 | 0,952918 |
Resultados principais: diferença máxima, réplicas, total de ensaios, poder alvo, poder real
Nestes resultados, o Minitab calcula o número de réplicas para atingir um poder alvo de 80% e um poder alvo de 90%. Para detectar uma diferença de 2,0, o experimento exige 3 réplicas para alcançar um alvo de 80% ou um alvo de 90%. O poder para o experimento com 2 réplicas é menor do que o poder alvo de 80%. Para detectar a menor diferença de 1,8, 3 réplicas proporcionam mais de 80% do poder, mas não mais do que 90% de poder. Para detectar a menor diferença com poder de 90%, o experimento planejado precisa de 4 réplicas. Como os números de réplicas são inteiros, os poderes reais são maiores do que os poderes alvo.
Estes resultados também mostram que o fator com a maioria dos níveis tem 4 níveis. Estes resultados são precisos para o fator de 4 níveis. O número de réplicas pode ser diferente para os dois fatores de 3 níveis, especialmente se o poder efetivo for muito maior do que o poder alvo.
Etapa 2: Examine a curva de poder
Use a curva de poder para avaliar as propriedades adequadas para o seu experimento.
A curva de poder representa a relação entre o poder e a diferença máxima para cada número de réplicas. Cada símbolo na curva de poder representa um valor calculado com base nas propriedades inseridas. Por exemplo, se você digitar um número de réplicas e um valor de poder, o Minitab calcula a diferença máxima correspondente e exibe o valor calculado no gráfico.
Examine os valores na curva para determinar a diferença entre as maiores e menores médias para o fator com o maior número de níveis que o experimento detecta a um determinado valor de poder e número de réplicas. Em geral, um valor de poder de 0,9 é considerado adequado. No entanto, alguns profissionais consideram o valor de poder de 0,8 como adequado. Se um experimento tem baixo poder, talvez não seja possível detectar uma diferença praticamente significativa. O aumento do número total de ensaios experimentais aumenta o poder de seu experimento. Você deseja ensaios experimentais suficientes em seu experimento para alcançar o poder adequado. Um experimento tem mais poder para detectar uma diferença maior que uma diferença menor.
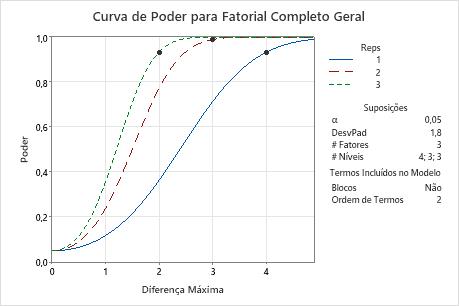
Nestes resultados, o Minitab calcula o número de réplicas, para alcançar um poder de pelo menos 0,9 para diferenças máximas de 2, 3 ou 4. O gráfico tem uma curva para cada número de réplicas. Para detectar uma diferença máxima de 2 com um poder de pelo menos 0,9, o experimento necessita de 3 réplicas. O gráfico contém uma curva para 3 réplicas e mostra um símbolo com uma diferença máxima de 2, onde o poder excede 0,9. Para detectar uma diferença máxima de 3 com, poder de pelo menos 0,9, o experimento necessita de 2 réplicas. Para uma diferença máxima de 4 com, poder de pelo menos 0,9, o experimento necessita de uma réplica.
