Neste tópico
Nível de significância (α)
O nível de significância (indicado por alfa ou α) é o nível de risco máximo aceitável para um erro de tipo I.
Interpretação
Use o nível de significância para determinar se a diferença é estatisticamente significativa. Como o nível de significância é o limite para significância estatística, um valor mais alto aumenta a chance de cometer um erro do tipo I. Um erro do tipo I é a conclusão incorreta de que existe uma diferença entre as médias em diferentes níveis de fator.
Desvio padrão suposto
O desvio padrão suposto a estimativa do desvio padrão das medições de resposta em ensaios experimentais replicados. Se você já fez uma análise do Minitab que produziu uma tabela ANOVA, pode usar a raiz quadrada do quadrado médio ajustado para erro.
Interpretação
Use o desvio padrão suposto para descrever como são os dados variáveis. Os valores mais elevados do desvio padrão suposto indicam mais variação ou "ruído" nos dados, o que diminui o poder estatístico de um experimento.
Fatores
O número mostra quantos fatores estão no experimento.
Interpretação
Use o número de fatores para se certificar de que o experimento tem todos os fatores que você precisa estudar. Fatores são as variáveis que você controla no experimento. Fatores também são conhecidos como variáveis independentes, variáveis explicativas e variáveis preditoras. Fatores podem assumir apenas um número limitado de valores possíveis, conhecidos como níveis de fator. Para um experimento fatorial completo geral, todos os fatores são categóricos.
Por exemplo, você está estudando fatores que poderiam afetar a resistência do plástico durante o processo de fabricação. Você decide incluir aditivo em sua experiência. O aditivo é uma variável categórica que pode ser do tipo A ou tipo B.
}Número de níveis
A lista mostra o número de níveis de cada um dos fatores que está no experimento.
Interpretação
Use o número de níveis para se certificar de que o experimento tem todos os fatores que você precisa estudar. Por exemplo, você está estudando fatores que poderiam afetar a resistência do plástico durante o processo de fabricação. Você decide incluir um fator sobre um aditivo. O aditivo é uma variável categórica. O aditivo pode ser do tipo A ou B. O número de níveis para o fator para aditivo é 2.
Incluir termos no modelo por toda a ordem
A ordem do modelo é o mais alto nível de interação que o Minitab usa para determinar o número de termos.
Interpretação
Use a ordem do modelo para verificar o modelo que os cálculos de poder assumem. Por exemplo, para estudar a interação entre 3 fatores, a ordem do modelo pode ser 3 ou mais.
Quanto mais alta a ordem, mais termos há no modelo. Os modelos com mais termos têm menos graus de liberdade para erro. Assim, os experimentos com mais termos têm menor poder que experimentos com menos termos quando todas as outras propriedades são as mesmas. Se você executar um cálculo em que a ordem do modelo é a mesmo que o número de fatores, os cálculos requerem mais do que uma replicação.
Nestes resultados, os cálculos de poder são para o modelo com termos que vão até a ordem 3. O número de fatores também é 3. Como este modelo usa todos os graus de liberdade de uma única replicação do experimento, o Minitab não calcula o poder para uma única replicação. Se você executar o mesmo cálculo para termos up até a ordem 2, é possível calcular o poder para uma replicação.
Resultados
| Diferença Máxima | Reps | Total de Ensaios | Poder |
|---|---|---|---|
| 2 | 3 | 108 | 0,930642 |
| 3 | 3 | 108 | 0,999667 |
Diferença máxima
A diferença máxima é a diferença que você deseja detectar entre os níveis de fatores que têm as médias mais altas e mais baixas. Os cálculos usam o fator que tem a maioria dos níveis para produzir os cálculos que são conservadores para outros fatores. O Minitab calcula a menor diferença de que o experimento detecta. Mais réplicas dão ao experimento a capacidade de detectar diferenças menores. Normalmente, você quer ser capaz de detectar a menor diferença que tem consequências práticas para a sua aplicação.
Interpretação
Use a diferença máxima para determinar quais as diferenças o experimento planejado detecta. Se você inserir um número de réplicas e um valor de poder, o Minitab calcula a diferença máxima. Normalmente, mais réplicas permitem detectar uma diferença máxima menor. Em geral, quanto mais réplicas, menor a diferença máxima que o experimento planejado detecta.
Nestes resultados, o experimento com uma réplica pode detectar uma diferença de aproximadamente 3,8 com 90% de poder. O experimento com 3 réplicas pode detectar uma diferença menor, com poder de 90%, aproximadamente 1,9.
Estes resultados também mostram que o fator com a maioria dos níveis tem 4 níveis. A diferença máxima calculada é exata para o fator de 4 níveis. A diferença máxima para o fator 4 de níveis é maior do que a diferença máxima para as duas de 3 níveis
Resultados
| Reps | Total de Ensaios | Poder | Diferença Máxima |
|---|---|---|---|
| 1 | 36 | 0,9 | 3,77758 |
| 3 | 108 | 0,9 | 1,88781 |
Réplicas
Réplicas são vários ensaios experimentais com as mesmas configurações de fatores.
Interpretação
Use o número de réplicas para estimar quantos ensaios experimentais devem ser incluídos no experimento. Se você inserir um poder e a diferença máxima, o Minitab calcula o número de réplicas. Como o número de réplicas é dado em valores inteiros, o poder real pode ser maior do que o valor alvo. Se você aumentar o número de réplicas, o poder de seu experimento também aumenta. Você deseja réplicas suficientes para alcançar o poder adequado.
Como as réplicas são valores inteiros, os valores de poder que você especifica são valores de poder alvo. Os valores de poder reais são para o número de réplicas e o número de pontos centrais no experimento planejado. Os valores de poder reais são no mínimo tão grandes quanto os valores de poder alvo.
Nestes resultados, o Minitab calcula o número de réplicas para atingir um poder alvo de 80% e um poder alvo de 90%. Para detectar uma diferença de 2,0, o experimento exige 3 réplicas para alcançar um alvo de 80% ou um alvo de 90%. O poder para o experimento com 2 réplicas é menor do que o poder alvo de 80%. Para detectar a menor diferença de 1,8, 3 réplicas proporcionam mais de 80% do poder, mas não mais do que 90% de poder. Para detectar a menor diferença com poder de 90%, o experimento planejado precisa de 4 réplicas. Como os números de réplicas são inteiros, os poderes reais são maiores do que os poderes alvo.
Estes resultados também mostram que o fator com a maioria dos níveis tem 4 níveis. Estes resultados são precisos para o fator de 4 níveis. O número de réplicas pode ser diferente para os dois fatores de 3 níveis, especialmente se o poder efetivo for muito maior do que o poder alvo.
Resultados
| Diferença Máxima | Reps | Total de Ensaios | Poder Alvo | Poder Real |
|---|---|---|---|---|
| 2,0 | 3 | 108 | 0,8 | 0,932615 |
| 2,0 | 3 | 108 | 0,9 | 0,932615 |
| 1,8 | 3 | 108 | 0,8 | 0,867493 |
| 1,8 | 4 | 144 | 0,9 | 0,952918 |
Ensaios totais
Um ensaio experimental é uma combinação de níveis de fatores em que você mede as respostas. O número total de ensaios é a forma como muitas medidas da resposta estão no experimento. Várias execuções da mesma combinação de níveis de fatores são considerados ensaios experimentais separados e são chamados réplicas.
Interpretação
Use o número total de ensaios para verificar se o experimento planejado é o tamanho certo para os seus recursos.

| Termo | Descrição |
|---|---|
| n | Número de réplicas |
| Li | Número de níveis no io fator |
| k | Número de fatores |
Nestes resultados, o experimento tem um fator de 4 níveis e dois fatores 3 níveis. O número de ensaios em uma única réplica é 4*3*3 = 36. Cada réplica acrescenta o mesmo número de ensaios. Assim, o número de ensaios em 3 réplicas de um ensaio de execução de 36 experimentos de execução experimental é de 36*3 = 108. Experimentos com mais ensaios experimentais têm mais poder para detectar uma diferença.
Resultados
| Diferença Máxima | Reps | Total de Ensaios | Poder |
|---|---|---|---|
| 2,5 | 1 | 36 | 0,539953 |
| 2,5 | 3 | 108 | 0,992993 |
Poder
O poder de um experimento fatorial completo geral é a probabilidade de que o efeito principal para o fator com maior número de níveis seja estatisticamente significativo. A diferença está entre as maiores e menores médias da variável de resposta para o fator com maior número de níveis. Os cálculos de poder são conservadores para fatores com menos níveis que estão no mesmo experimento.
Interpretação
Use o valor de poder para determinar a capacidade do experimento para detectar a diferença. Se você inserir um número de réplicas e uma diferença máxima, o Minitab calcula o poder do experimento. Em geral, um valor de poder de 0,9 é considerado adequado. Um valor de 0,9 indica que você tem uma probabilidade de 90% de detectar a diferença entre os níveis de fatores se a diferença for o tamanho especificado por você. Em geral, quando o número de réplicas é menor, o poder é baixo. Se um experimento apresentar baixo poder, talvez não seja possível detectar a diferença e você conclua erroneamente que não existe nenhuma.
Estes resultados demonstram como o aumento do número de réplicas aumenta o poder. Para uma diferença de 2, o poder do experimento é de aproximadamente 0,36 com uma réplica. Com 3 réplicas, o poder aumenta para aproximadamente 0,93.
Estes resultados também demonstram como o aumento do tamanho do efeito aumenta o poder. Para um experimento com uma réplica e uma diferença de 2, o poder é de aproximadamente 0,36. Para uma experiência com uma réplica e uma diferença de 3, o poder é de aproximadamente 0,71.
Resultados
| Diferença Máxima | Reps | Total de Ensaios | Poder |
|---|---|---|---|
| 2 | 1 | 36 | 0,362893 |
| 2 | 3 | 108 | 0,932615 |
| 3 | 1 | 36 | 0,712094 |
| 3 | 3 | 108 | 0,999695 |
Curva de poder
A curva de poder representa graficamente o poder do teste versus a diferença máxima. A diferença máxima refere-se à diferença entre as maiores e menores médias para o fator com o maior número de níveis. Os cálculos de poder são conservadoras para fatores com menos níveis que estão no mesmo projeto.
Interpretação
Use a curva de poder para avaliar as propriedades adequadas para o seu experimento.
A curva de poder representa a relação entre o poder e a diferença máxima para cada número de réplicas. Cada símbolo na curva de poder representa um valor calculado com base nas propriedades inseridas. Por exemplo, se você digitar um número de réplicas e um valor de poder, o Minitab calcula a diferença máxima correspondente e exibe o valor calculado no gráfico.
Examine os valores na curva para determinar a diferença entre as maiores e menores médias para o fator com o maior número de níveis que o experimento detecta a um determinado valor de poder e número de réplicas. Em geral, um valor de poder de 0,9 é considerado adequado. No entanto, alguns profissionais consideram o valor de poder de 0,8 como adequado. Se um experimento tem baixo poder, talvez não seja possível detectar uma diferença praticamente significativa. O aumento do número total de ensaios experimentais aumenta o poder de seu experimento. Você deseja ensaios experimentais suficientes em seu experimento para alcançar o poder adequado. Um experimento tem mais poder para detectar uma diferença maior que uma diferença menor.
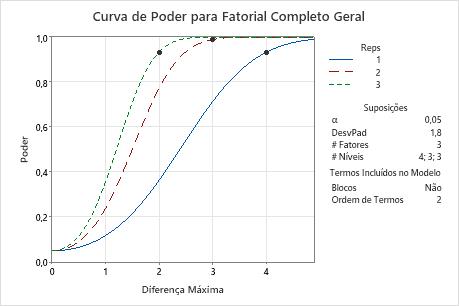
Nestes resultados, o Minitab calcula o número de réplicas, para alcançar um poder de pelo menos 0,9 para diferenças máximas de 2, 3 ou 4. O gráfico tem uma curva para cada número de réplicas. Para detectar uma diferença máxima de 2 com um poder de pelo menos 0,9, o experimento necessita de 3 réplicas. O gráfico contém uma curva para 3 réplicas e mostra um símbolo com uma diferença máxima de 2, onde o poder excede 0,9. Para detectar uma diferença máxima de 3 com, poder de pelo menos 0,9, o experimento necessita de 2 réplicas. Para uma diferença máxima de 4 com, poder de pelo menos 0,9, o experimento necessita de uma réplica.
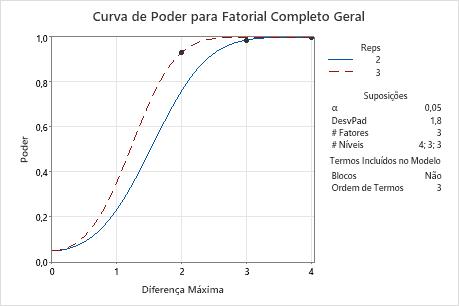
Compare a curva de poder para uma ordem de termos de 3 com a curva de poder para uma ordem de termos de 2. A solução com 1 réplica é possível apenas quando a ordem de termos é menor do que o número de fatores. Se o número de fatores for igual à ordem de termos, um experimento para 1 réplica não terá graus suficientes de liberdade para o cálculo de poder. Nos resultados, a ordem de termos é 3 e o número de fatores é 3, de modo que o experimento para 1 réplica não é uma solução viável. A solução, quando a diferença máxima é de 4, torna-se o experimento para 2 réplicas.
