Etapa 1: Examine os valores calculados
Usando os valores de três variáveis de função de poder que você inseriu, o Minitab calcula o número de réplicas, o tamanho do efeito, o poder do experimento ou o número de pontos centrais.
- Efeito
-
Se você inserir o numero de réplicas, o valor do poder e o número de pontos centrais, o Minitab calcula o efeito. O efeito é a diferença entre as médias da variável resposta aos níveis altos e baixos de um fator que você deseja que o experimento detecte. Esta diferença pode ser o resultado de um fator sozinho (efeito principal) ou de uma combinação de fatores (interação).
- Pontos centrais
-
Se você inserir o número de réplicas, o tamanho do efeito e o valor de poder, o Minitab calcula o número de pontos centrais. Pontos centrais são ensaios experimentais com todos os níveis de fator definidos no ponto médio entre a configuração baixa e alta. Os pontos centrais são utilizados principalmente para detectar efeitos de curvatura, mas a adição de mais pontos centrais pode também aumentar um pouco o poder.
- Réplicas
- Se você inserir o tamanho do efeito, o valor do poder e o número de pontos centrais, o Minitab calcula o número de réplicas. Réplicas são vários ensaios experimentais com as mesmas configurações de fatores. Como o número de réplicas é um valor inteiro, o poder real pode ser um pouco maior do que seu valor alvo.
- Ensaios totais
- Para cada caso, o Minitab calcula o total de ensaios a partir do número de réplicas e o número de pontos centrais. O número total de ensaios é o produto do número de pontos de extremidade e o número de réplicas, mais o produto do número de pontos centrais por bloco e o número de blocos.
- Valores de poder
- Se você digitar o número de replicações, o tamanho do efeito, e o número de pontos centrais, o Minitab calcula o valor de poder. O poder é a probabilidade de que você encontre corretamente um efeito significativo. Em geral, um valor de poder de 0,9 é considerado suficiente. Um valor de 0,9 indica que há uma probabilidade de 90% de detecção de um efeito. Normalmente, quando o número total de ensaios é menor ou o efeito é menor, o experimento tem menos poder.
Método
| Fatores: | 15 | Experimento Base: | 15; 32 |
|---|---|---|---|
| Blocos: | nenhum |
Resultados
| Pontos Centrais | Efeito | Reps | Total de Ensaios | Poder Alvo | Poder Real |
|---|---|---|---|---|---|
| 0 | 2,0 | 1 | 32 | 0,8 | 0,877445 |
| 0 | 2,0 | 2 | 64 | 0,9 | 0,995974 |
| 0 | 0,9 | 4 | 128 | 0,8 | 0,843529 |
| 0 | 0,9 | 5 | 160 | 0,9 | 0,914018 |
Resultados principais: pontos centrais, efeito, réplicas, efeitos totais, poder alvo, poder real
Nestes resultados, o Minitab calcula o número de réplicas, para atingir o poder alvo. O experimento que detecta um efeito de 2 com um poder de 0,8 requer 1 réplica. Para atingir um poder de 0,9, o experimento requer 2 réplicas. O poder real com 2 réplicas é maior do que 0,99. Este poder real é o menor valor de poder que é maior ou igual a 0,9 e é obtido usando-se um número inteiro de réplicas. Para detectar o menor efeito de 0,9 com poder 0,8, o experimento necessita de 4 réplicas. Para detectar o menor efeito de 0,9 com poder 0,9, o experimento requer 5 réplicas.
Etapa 2: Examine a curva de poder
Use a curva de poder para avaliar as propriedades adequadas para o seu experimento.
A curva de poder representa a relação entre poder e tamanho do efeito para todas as combinação de pontos centrais e repetições. Cada símbolo na curva da poder representa um valor calculado com base nas propriedades que você insere. Por exemplo, se você inserir um número de réplicas, um valor de poder e um número de pontos centrais, o Minitab calcula o tamanho do efeito correspondente e exibe o valor calculado no gráfico para a combinação de réplicas e pontos centrais. Se você resolver para réplicas ou pontos centrais, o gráfico também inclui curvas para as outras combinações de réplicas e pontos centrais que estão nas combinações que alcançam o poder de destino. O gráfico não mostra curvas para casos que não têm graus de liberdade suficientes para avaliar a significância estatística.
Examine os valores na curva para determinar o tamanho de efeito que o experimento detecta a um determinado poder, número de pontos de extremidades e número de pontos centrais. Em geral, um valor de poder de 0,9 é considerado adequado. No entanto, alguns profissionais consideram o valor de poder de 0,8 como adequado. Se uma experimento com um fator tiver baixo poder, talvez não seja possível detectar um efeito que seja praticamente significativo. Aumentar o número de réplicas aumenta o poder de seu experimento. Você quer ensaios experimentais suficientes em seu experimento para alcançar o poder adequado. Um experimento tem mais poder para detectar um efeito maior do que um efeito menor.
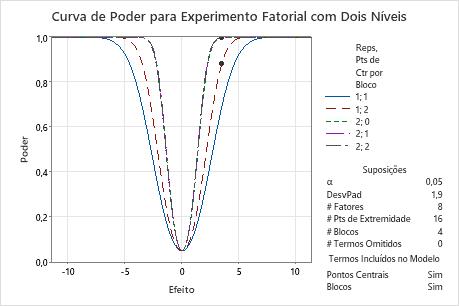
Nestes resultados, o Minitab calcula o número de réplicas, para atingir um alvo de poder de pelo menos 0,8 ou 0,9 para um tamanho de efeito de 3,5. O experimento planejado tem 16 pontos de extremidade em 4 blocos para estudar 4 fatores. Os cálculos consideram experimentos planejados com 0, 1 ou 2 pontos centrais por bloco. A curva que mostra uma réplica e dois pontos centrais tem um símbolo para o efeito de 3,5 onde o poder é superior ao poder do alvo de 0,8. As três curvas que representam os experimentos com 2 réplicas têm símbolos que mostram que o poder para detectar um efeito de 3,5 que excede o poder do alvo de 0,9.
Como existe uma solução com 2 réplicas e um ponto central e existe uma solução com 1 réplica e 2 pontos centrais, o gráfico também inclui uma curva para um experimento com uma réplica e um ponto central. Este experimento não pode atingir nenhum alvo para o efeito de 3,5, de modo que esta curva não tem um símbolo. O gráfico não inclui o símbolo com uma réplica e 0 pontos centrais, pois este experimento não tem graus de liberdade suficientes para avaliar a significância estatística quando 0 termos são omitidos do modelo.
