Neste tópico
Nível de significância (α)
O nível de significância (indicado por alfa ou α) é o nível de risco máximo aceitável para um erro de tipo I.
Interpretação
Use o nível de significância para determinar se um efeito é estatisticamente significativo. Como o nível de significância é o limite para significância estatística, um valor mais alto aumenta a chance de cometer um erro do tipo I. Um erro do tipo I é a conclusão incorreta de que um efeito é estatisticamente significativo.
Desvio padrão suposto
O desvio padrão suposto a estimativa do desvio padrão das medições de resposta em ensaios experimentais replicados. Se você já fez uma análise do Minitab que produziu uma tabela ANOVA, pode usar a raiz quadrada do quadrado médio ajustado para erro.
Interpretação
Use o desvio padrão suposto para descrever como são os dados variáveis. Os valores mais elevados do desvio padrão suposto indicam mais variação ou "ruído" nos dados, o que diminui o poder estatístico de um experimento.
Fatores
O número mostra quantos fatores estão no experimento.
Interpretação
Use o número de fatores para se certificar de que o experimento tem todos os fatores que você precisa estudar. Fatores são variáveis que você controla no experimento. Fatores também são conhecidos como variáveis independentes, variáveis explicativas e variáveis de preditoras. Para os cálculos de poder e tamanho de amostra, todos os fatores são numéricos. Fatores numéricos usam alguns valores controlados no experimento, embora muitos valores sejam possíveis. Esses valores são conhecidos como os níveis de fator.
Por exemplo, você está estudando fatores que poderiam afetar a resistência do plástico durante o processo de fabricação. Você decide incluir Temperatura em seu experimento. Como a temperatura é um fator, apenas três configurações de temperaturas estão no experimento: 100 °C, 150 °C e 200 °C.
Experimento base
Os números indicam o número de fatores e o número de pontos de extremidade no experimento de base.
Interpretação
Use o experimento base para determinar se o projeto experimental é um experimento inteiro ou um experimento fracionado. Se o número de pontos de extremidade for inferior a 2^(número de fatores), o projeto experimental é um experimento fracionado. Em um experimento fracionado, nem todos os termos que o experimento pode estimar são independentes uns dos outros. Para ver como os termos dependem uns dos outros, crie o experimento e revise a tabela de aliases.
O experimento base é o ponto de partida a partir do qual você pode construir seu experimento final. É possível adicionar ao experimento de base para atingir diferentes finalidades. Por exemplo, você pode adicionar réplicas ou pontos centrais para aumentar o poder do experimento.
Blocos
O número mostra quantos blocos estão no experimento.
Interpretação
Utilize este número de blocos para identificar o experimento que os cálculos de poder usam. Blocos são grupos de ensaios experimentais realizados sob condições relativamente homogêneas. Embora cada medição deva ser realizada sob condições experimentais constantes (com exceção daquelas que são variadas como parte do experimento), isso nem sempre é possível.
Por exemplo, você quer testar a qualidade de uma nova prensa de impressão. No entanto, a configuração da prensa leva várias horas e só pode ser feita quatro vezes por dia. Como o planejamento do experimento requer pelo menos oito ensaios, são necessários pelo menos dois dias para testar a prensa. Todas diferenças nas condições entre dias usando "dia" como uma variável de bloqueio devem ser levadas em consideração. Para distinguir entre qualquer efeito de bloco (diferenças acidentais entre os dias) e os efeitos devido aos fatores experimentais (temperatura, umidade e operador da prensa), leve em conta o bloco (dia) no planejamento experimental. Você deve aleatorizar a ordem de execução dentro de blocos. Para obter mais informações sobre como o Minitab atribui execuções a blocos, acesse O que é um bloco?
Pontos centrais por bloco
O número mostra quantos pontos centrais por bloco estão no experimento.
Interpretação
Use o número de pontos centrais por bloco para identificar o experimento que os cálculos de poder usam. Os pontos centrais são ensaios onde todos os fatores são fixados a meio caminho entre os níveis baixo e alto. Se o experimento inclui blocos, o Minitab adiciona o mesmo número de pontos centrais para cada bloco. Por exemplo, se você especificar 2 pontos centrais por bloco e 2 blocos, o experimento inclui 4 pontos centrais.
Em geral, os pontos centrais exercem uma pequena influência sobre os resultados quando o experimento inclui réplicas dos pontos de extremidade. Os pontos centrais têm outras utilizações além da sua influência sobre os cálculos de poder. Por exemplo, o teste para curvatura na resposta requer pontos centrais.
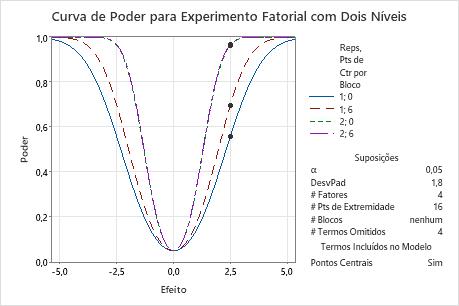
Nestes resultados, os pontos das curvas de poder mostram cálculos para uma diferença de 2,5. O experimento com 1 réplica e nenhum ponto central tem um poder próximo a 0,56. O experimento com 1 réplica e 6 pontos centrais tem um poder de quase 0,7. Com duas réplicas, as curvas de poder de 0 pontos centrais e 6 pontos centrais são indistinguíveis no gráfico. A curva para 6 pontos centrais é um pouco superior para efeitos diferentes de zero. Os valores de poder são ambos maiores que 0,95.
Método
| Fatores: | 4 | Experimento Base: | 4; 16 |
|---|---|---|---|
| Blocos: | nenhum |
Resultados
| Pontos Centrais | Efeito | Reps | Total de Ensaios | Poder |
|---|---|---|---|---|
| 0 | 2,5 | 1 | 16 | 0,557255 |
| 0 | 2,5 | 2 | 32 | 0,961939 |
| 6 | 2,5 | 1 | 22 | 0,696490 |
| 6 | 2,5 | 2 | 38 | 0,965121 |
Efeito
Se você inserir o número de réplicas, o valor do poder e o número de pontos centrais, o Minitab calcula o efeito. O efeito é a diferença na resposta entre os níveis altos e baixos de um fator que você deseja que o experimento detecte. Esta diferença é o resultado de um fator de sozinho (efeito principal).
Interpretação
Usar o tamanho do efeito para determinar a capacidade do experimento para detectar um efeito. Se você digitar um número de réplicas, um poder e um número de pontos centrais, o Minitab calcula o menor tamanho de efeito que o experimento pode detectar com o poder especificado. Normalmente, mais réplicas permitem que um experimento planejado detecte efeitos menores.
Nestes resultados, o experimento com uma réplica pode detectar uma diferença de aproximadamente 0,015 com 80% de poder. A diferença que o experimento pode detectar com 90% de poder é maior do que 0,015, aproximadamente 0,018. O experimento com 2 réplicas pode detectar uma diferença que é menor do que 0,015, com 80% de poder, aproximadamente 0,007.
Método
| Fatores: | 5 | Experimento Base: | 5; 32 |
|---|---|---|---|
| Blocos: | nenhum |
Resultados
| Pontos Centrais | Reps | Total de Ensaios | Poder | Efeito |
|---|---|---|---|---|
| 4 | 1 | 36 | 0,8 | 0,0153027 |
| 4 | 1 | 36 | 0,9 | 0,0180278 |
| 4 | 2 | 68 | 0,8 | 0,0073261 |
| 4 | 2 | 68 | 0,9 | 0,0084775 |
Réplicas
Réplicas são vários ensaios experimentais com as mesmas configurações de fatores.
Interpretação
Use o número de réplicas para estimar quantos ensaios experimentais devem ser incluídos no experimento. Se você inserir um poder, tamanho de efeito e o número de pontos centrais, o Minitab calcula o número de réplicas. Como o número de réplicas e pontos centrais é dado em valores inteiros, o poder real pode ser maior do que seu valor alvo. Se você aumentar o número de réplicas, o poder de seu experimento também aumenta. Você deseja réplicas suficientes para alcançar o poder adequado.
Como as réplicas são valores inteiros, os valores de poder que você especifica são valores de poder alvo. Os valores de poder reais são para o número de réplicas e o número de pontos centrais no experimento planejado. Os valores de poder reais são no mínimo tão grandes quanto os valores de poder alvo.
Nestes resultados, o Minitab calcula o número de réplicas, para atingir o poder alvo. O experimento que detecta um efeito de 2 com um poder de 0,8 requer 1 réplica. Para atingir um poder de 0,9, o experimento requer 2 réplicas. O poder real com 2 réplicas é maior do que 0,99. Este poder real é o menor valor de poder que é maior ou igual a 0,9 e é obtido usando-se um número inteiro de réplicas. Para detectar o menor efeito de 0,9 com poder 0,8, o experimento necessita de 4 réplicas. Para detectar o menor efeito de 0,9 com poder 0,9, o experimento requer 5 réplicas.
Método
| Fatores: | 15 | Experimento Base: | 15; 32 |
|---|---|---|---|
| Blocos: | nenhum |
Resultados
| Pontos Centrais | Efeito | Reps | Total de Ensaios | Poder Alvo | Poder Real |
|---|---|---|---|---|---|
| 0 | 2,0 | 1 | 32 | 0,8 | 0,877445 |
| 0 | 2,0 | 2 | 64 | 0,9 | 0,995974 |
| 0 | 0,9 | 4 | 128 | 0,8 | 0,843529 |
| 0 | 0,9 | 5 | 160 | 0,9 | 0,914018 |
Compare o primeiro conjunto de resultados com o segundo conjunto de resultados. No primeiro conjunto de resultados, 16 termos são omitidos do modelo. No segundo conjunto de resultados, o modelo inclui todos os termos estimáveis. Como o segundo modelo utiliza todos os graus de liberdade para uma única réplica do experimento, o Minitab não inclui uma réplica como solução. Como o número de termos no modelo é mais elevado, os outros valores de poder são mais baixos do que nos resultados, onde o modelo omite termos. Por exemplo, o poder real para o experimento com 5 réplicas é de aproximadamente 0,9140 no primeiro conjunto de resultados e aproximadamente 0,9136 no segundo conjunto de resultados.
Método
| Fatores: | 15 | Experimento Base: | 15; 32 |
|---|---|---|---|
| Blocos: | nenhum |
Resultados
| Pontos Centrais | Efeito | Reps | Total de Ensaios | Poder Alvo | Poder Real |
|---|---|---|---|---|---|
| 0 | 2,0 | 2 | 64 | 0,8 | 0,995347 |
| 0 | 2,0 | 2 | 64 | 0,9 | 0,995347 |
| 0 | 0,9 | 4 | 128 | 0,8 | 0,842492 |
| 0 | 0,9 | 5 | 160 | 0,9 | 0,913575 |
Ensaios totais
Um ensaio experimental é uma combinação de níveis de fatores em que você mede as respostas. O número total de ensaios é a forma como muitas medidas da resposta estão no experimento. Várias execuções da mesma combinação de níveis de fatores são considerados ensaios experimentais separados e são chamados réplicas.
Interpretação
Use o número total de ensaios para verificar se o experimento planejado é o tamanho certo para os seus recursos. Para um experimento fatorial de 2 níveis, esta fórmula fornece o número total de ensaios experimentais:

| Termo | Descrição |
|---|---|
| n | Número de réplicas |
| r | Número de pontos de extremidade por réplica |
| cpblock | Número de pontos centrais por bloco |
| b | Número de blocos |
Nestes resultados, o experimento base tem 16 pontos de extremidade. O experimento tem 4 blocos e 4 pontos centrais por bloco, para um total de 4 * 4 = 16 pontos centrais. Assim, o experimento com uma réplica tem 16 pontos de extremidade e 16 pontos centrais para um total de 16 + 16 = 32 ensaios experimentais. O ensaios com 2 réplicas dobra o número de pontos de extremidade para 2 * 16 = 32. O número de blocos e o número de pontos centrais por bloco permanece o mesmo. Como resultado, o experimento com 2 réplicas tem um total de 32 + 16 = 48 ensaios.
Método
| Fatores: | 4 | Experimento Base: | 4; 16 |
|---|---|---|---|
| Blocos: | 4 |
Resultados
| Pontos Centrais por Bloco | Efeito | Reps | Total de Ensaios | Poder |
|---|---|---|---|---|
| 4 | 2,5 | 1 | 32 | 0,741569 |
| 4 | 2,5 | 2 | 48 | 0,967699 |
Poder
O poder de um experimento é a probabilidade de que o experimento determine que um efeito seja estatisticamente significativo. A diferença entre as médias da variável de resposta aos níveis altos e baixos de um fator é o tamanho do efeito.
Interpretação
Use o valor de poder para determinar a capacidade de o experimento detectar um efeito. Se você inserir um número de replicações, um tamanho de efeito, e um número de pontos centrais, o Minitab calcula o poder do experimento. Em geral, um valor de poder de 0,9 é considerado adequado. Um valor de 0,9 indica que um experimento tem uma probabilidade de 90% de detectar um efeito do tamanho que você especificar. Normalmente, quanto menor o número de replicações, menor é a potência. Se um experimento tiver baixo poder, você pode deixar de detectar um efeito e erroneamente concluir que não existe nenhum.
Estes resultados demonstram como o aumento do número de ensaios experimentais aumenta o poder. Para um tamanho de efeito de 0,9, o poder do experimento é de aproximadamente 0,55 com 64 ensaios no total. Com 160 ensaios no total o poder do experimento aumenta para cerca de 0,91.
Estes resultados também demonstram como o aumento do tamanho do efeito aumenta o poder. Para um experimento de 64 ensaios, o poder é de aproximadamente 0,55 para um tamanho de efeito de 0,9. Com um tamanho de efeito de 1,5, o poder aumenta para cerca de 0,93.
Método
| Fatores: | 15 | Experimento Base: | 15; 32 |
|---|---|---|---|
| Blocos: | nenhum |
Resultados
| Pontos Centrais | Efeito | Reps | Total de Ensaios | Poder |
|---|---|---|---|---|
| 0 | 1,5 | 5 | 160 | 0,999830 |
| 0 | 1,5 | 2 | 64 | 0,932932 |
| 0 | 0,9 | 5 | 160 | 0,914018 |
| 0 | 0,9 | 2 | 64 | 0,545887 |
Curva de poder
A curva de poder representa graficamente o poder do experimento versus o tamanho do efeito. Efeito se refere à diferença entre o valor da resposta média nos níveis alto e baixo de um fator.
Interpretação
Use a curva de poder para avaliar as propriedades adequadas para o seu experimento.
A curva de poder representa a relação entre poder e tamanho do efeito para todas as combinação de pontos centrais e repetições. Cada símbolo na curva da poder representa um valor calculado com base nas propriedades que você insere. Por exemplo, se você inserir um número de réplicas, um valor de poder e um número de pontos centrais, o Minitab calcula o tamanho do efeito correspondente e exibe o valor calculado no gráfico para a combinação de réplicas e pontos centrais. Se você resolver para réplicas ou pontos centrais, o gráfico também inclui curvas para as outras combinações de réplicas e pontos centrais que estão nas combinações que alcançam o poder de destino. O gráfico não mostra curvas para casos que não têm graus de liberdade suficientes para avaliar a significância estatística.
Examine os valores na curva para determinar o tamanho de efeito que o experimento detecta a um determinado poder, número de pontos de extremidades e número de pontos centrais. Em geral, um valor de poder de 0,9 é considerado adequado. No entanto, alguns profissionais consideram o valor de poder de 0,8 como adequado. Se uma experimento com um fator tiver baixo poder, talvez não seja possível detectar um efeito que seja praticamente significativo. Aumentar o número de réplicas aumenta o poder de seu experimento. Você quer ensaios experimentais suficientes em seu experimento para alcançar o poder adequado. Um experimento tem mais poder para detectar um efeito maior do que um efeito menor.
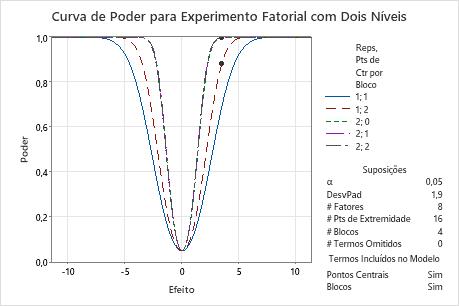
Nestes resultados, o Minitab calcula o número de réplicas, para atingir um alvo de poder de pelo menos 0,8 ou 0,9 para um tamanho de efeito de 3,5. O experimento planejado tem 16 pontos de extremidade em 4 blocos para estudar 4 fatores. Os cálculos consideram experimentos planejados com 0, 1 ou 2 pontos centrais por bloco. A curva que mostra uma réplica e dois pontos centrais tem um símbolo para o efeito de 3,5 onde o poder é superior ao poder do alvo de 0,8. As três curvas que representam os experimentos com 2 réplicas têm símbolos que mostram que o poder para detectar um efeito de 3,5 que excede o poder do alvo de 0,9.
Como existe uma solução com 2 réplicas e um ponto central e existe uma solução com 1 réplica e 2 pontos centrais, o gráfico também inclui uma curva para um experimento com uma réplica e um ponto central. Este experimento não pode atingir nenhum alvo para o efeito de 3,5, de modo que esta curva não tem um símbolo. O gráfico não inclui o símbolo com uma réplica e 0 pontos centrais, pois este experimento não tem graus de liberdade suficientes para avaliar a significância estatística quando 0 termos são omitidos do modelo.
