Etapa 1: Examine os valores calculados
Ao usar os valores das duas variáveis de função de poder que você inseriu, o Minitab calcula a razão, o tamanho amostral ou o poder do teste.
- Razão
-
O Minitab calcula a menor taxa que você poderá detectar com base na potência especificada e no tamanho da amostra. Tamanhos de amostra maiores permitem que você detecte proporções menores. Você quer ser capaz de detectar a menor proporção que tem consequências práticas para sua aplicação.
- Tamanho amostral
-
O Minitab calcula o tamanho que sua amostra deve ter para que um teste com seu poder especificado detecte a razão especificada. Como os tamanhos amostrais são números inteiros, o poder real do teste pode ser um pouco maior do que o valor de poder que você especificar.
Se você aumentar o tamanho amostral, o poder do teste também aumentará. Você quer observações suficientes na sua amostra para alcançar o poder adequado. Porém, você não quer um tamanho amostral tão grande a ponto de perder tempo e dinheiro em amostragens desnecessárias ou detectar diferenças sem importância para serem estatisticamente significativas.
- Poder
-
O Minitab calcula o poder do teste com base na taxa e tamanho amostral especificado. Em geral, um valor de poder de 0,9 é considerado adequado. Um valor de 0,9 indica que você tem uma probabilidade de 90% de detectar uma diferença entre duas variâncias da população ou desvios padrão quando uma diferença realmente existe. Se um teste apresenta baixo poder, talvez não seja possível detectar a diferença e você conclua erroneamente que não existe nenhuma. Normalmente, quando o tamanho amostral é menor ou a taxa é próxima de 1, o teste tem menos poder para detectar uma diferença.
Resultados
| Tamanho Amostral | Poder | Razão |
|---|---|---|
| 50 | 0,9 | 2,83320 |
| 50 | 0,9 | 0,35296 |
Resultados principais: razão, tamanho amostral, poder
Estes resultados mostram que, se o tamanho amostral for 50 e o valor de poder for igual a 0,9, o teste pode detectar razões aproximadamente 2,83 e 0,35. Se a sua situação exige que o teste seja capaz de detectar uma razão mais próxima de 1, é necessário aumente o tamanho amostral, se possível.
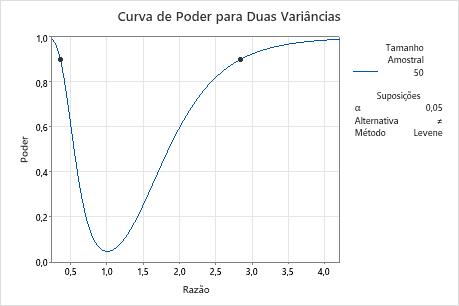
Etapa 2: Examine a curva de poder
Use a curva de poder para avaliar o tamanho amostral ou o poder adequado para o seu teste.
A curva de poder representa todas as combinações de poder e razão para cada tamanho amostral quando o nível de significância é mantido constante. Cada símbolo na curva de poder representa um valor calculado com base nos valores inseridos. Por exemplo, se você inserir um tamanho amostral e um valor de poder, o Minitab calcula a razão correspondente e exibe o valor calculado no gráfico.
Examine os valores na curva para determinar a razão que pode ser detectada a um determinado valor de poder e tamanho amostral. Em geral, um valor de poder de 0,9 é considerado adequado. No entanto, alguns profissionais consideram o valor de poder de 0,8 como adequado. Se um teste de hipótese tiver baixo poder, talvez não seja possível detectar a razão que é praticamente significativa. Se você aumentar o tamanho amostral, o poder do teste também aumentará. Você quer observações suficientes na sua amostra para alcançar o poder adequado. Porém, você não quer um tamanho amostral tão grande a ponto de perder tempo e dinheiro em amostragens desnecessárias ou detectar diferenças sem importância para serem estatisticamente significativas. Se você diminuir o tamanho da diferença que deseja detectar, o poder também diminuirá.
Neste gráfico, a curva de poder mostra que, para um tamanho amostral de 50 e um poder de 0,9, o teste pode detectar uma razão de aproximadamente 2,8 ou 0,35. À medida que a razão se aproxima de 1, o poder do teste diminui e se aproxima de α (também chamado o nível de significância), que é de 0,05 para esta análise.