Um engenheiro de uma empresa de cuidados com os olhos testa uma nova solução de limpeza para lentes de contato. O engenheiro quer verificar se a nova solução limpa as lentes, assim como a marca líder. O engenheiro faz um teste com 14 participantes usando lentes de contato por um dia e depois limpando essas lentes. Cada participante limpa uma lente com a nova solução e a outra com a marca líder. O engenheiro avalia a limpeza de cada lente medindo o ângulo de contato de uma gota de fluido na lente. O ângulo de contato é afetado por película ou depósitos nas lentes. Para ser equivalente, o ângulo médio para a nova solução deve estar dentro de ± 0,5 graus do ângulo médio da marca líder.
Antes de a engenheira coletar os dados para o teste de equivalência com dados pareados, ela usa um cálculo de poder e tamanho de amostra para determinar se um tamanho de amostra de 14 proporciona poder suficiente para o teste. A partir das amostras anteriores, a engenheira estima que o desvio padrão da população é 0,42.
- Selecione .
- Em Hipótese sobre, selecione Média de teste - média de referência (Diferença).
- Em O que você deseja determinar? (Hipótese alternativa), selecione Limite inferior < média de teste - média de referência < limite superior.
- Em Limite inferior, insira -0,5. Em Limite superior, insira 0,5.
- Em Tamanhos amostrais, insira 14.
- Em Diferenças (dentro dos limites), insira 0,1 0,2 0,3 0,4.
- Em Desvio padrão das diferenças pareadas, insira 0,42.
- Clique em OK.
Interpretar os resultados
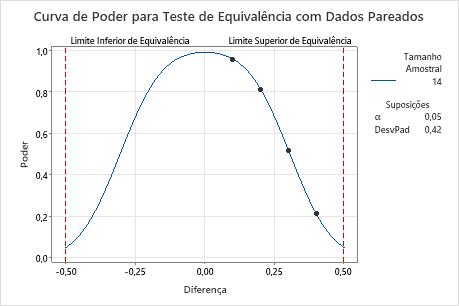
Se a diferença é de 0,1 e o engenheiro utiliza um tamanho amostral de 14 pares de observações, o poder do teste é maior do que 0,9. Se a diferença é for 0,2 e o engenheiro usa um tamanho amostral de 14 pares de observação, o teste tem um poder acima de 0,8. No entanto, se a diferença for de 0,3, e o engenheiro utilizar um tamanho amostral de 14 pares de observações, o teste terá um poder de aproximadamente 0,52, o que não é adequado.
Quando a diferença estiver mais próxima do limite de equivalência superior (0,5), a potência do teste é inferior. Por exemplo, para uma diferença de 0,4, se o engenheiro utiliza um tamanho amostral de 14 pares de observações, o teste tem um poder de aproximadamente 0,22.
Para qualquer amostra, como a diferença se aproxima do limite de equivalência inferior ou do limite de equivalência superior, o poder do teste diminui e se aproxima de α (alfa, que é o risco de afirmar a equivalência quando não ela não é verdadeira).
Método
| Poder para a diferença: | Média de teste - média de referência |
|---|---|
| Hipótese nula: | Diferença ≤ -0,5 ou Diferença ≥ 0,5 |
| Hipótese alternativa: | -0,5 < Diferença < 0,5 |
| Nível α: | 0,05 |
Resultados
| Diferença | Tamanho Amostral | Poder |
|---|---|---|
| 0,1 | 14 | 0,957371 |
| 0,2 | 14 | 0,811858 |
| 0,3 | 14 | 0,517255 |
| 0,4 | 14 | 0,211869 |