Métodos e fórmulas para Poder e tamanho de amostra para teste de equivalência para experimento cruzado 2x2

Este tópico descreve como o poder é calculado quando você seleciona Média de teste - média de referência (Diferença) em Hipótese sobre.

Poder

Permita que t_α,v seja o valor crítico α superior (unilateral) para uma distribuição t com v graus de liberdade. O poder para a hipótese alternativa bilateral de Limite inferior < média de teste - média de referência < limite superior é dado por:

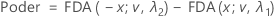
Para a hipótese alternativa de Média de teste > média de referência ou Média de teste - média de referência > limite inferior, o poder é dado por:

Para a hipótese alternativa de Média de teste < média de referência ou Média de teste - média de referência < limite superior, o poder é dado por:

onde FDA( x ; v , λ ) é a função de distribuição acumulada, avaliada em x, para uma distribuição t não central com o parâmetro de não centralidade, λ , e v graus de liberdade.

Graus de liberdade

Os graus de liberdade, v, são dados por:

Para os cálculos de poder, assume-se que, n seja o mesmo para ambas as sequências.

Parâmetros de não centralidade

O parâmetro de não centralidade que corresponde ao limite de equivalência inferior é denotado como λ₁ e é dado por:

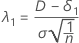
onde σ é o desvio padrão intra-sujeito.

Para a hipótese alternativa de Média de teste > média de referência, δ₁ = 0.

O parâmetro de não centralidade que corresponde ao limite superior equivalência é denotado como λ₂, e é dado pela seguinte fórmula:

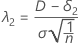
onde δ₂é o limite de equivalência superior.

Para a hipótese alternativa de Média de teste < média de referência, δ₂ = 0.

Notação

Termo	Descrição
α	nível de significância para o teste
D	média da população de teste menos a média da população de referência
δ1	limite de equivalência inferior
δ2	limite de equivalência superior
n	número de participantes em cada sequência. (Para os cálculos de poder, supõe-se que n é o mesmo para ambas as sequências).

Este tópico descreve como o poder é calculado quando você seleciona Média de teste / média de referência (Razão, por transformação de log) em Hipótese sobre.

Poder

Permita que t_α,v seja o valor crítico α superior (unilateral) para uma distribuição t com v graus de liberdade. O poder para a hipótese alternativa bilateral de Limite inferior < média de teste / média de referência < limite superior é dado por:

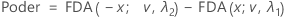
Para a hipótese alternativa de Média de teste / média de referência > limite inferior o poder é dado por:

Para a hipótese alternativa de Média de teste / média de referência < limite superior o poder é dado por:

onde FDA( x ; v , λ ) é a função de distribuição acumulada, avaliada em x, para uma distribuição t não central com o parâmetro de não centralidade, λ , e v graus de liberdade.

Graus de liberdade

Os graus de liberdade, v, são dados por:

Para os cálculos de poder, assume-se que, n seja o mesmo para ambas as sequências.

Parâmetros de não centralidade

O parâmetro de não centralidade que corresponde ao limite de equivalência inferior é denotado como λ₁ e é dado por:

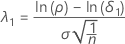
onde σ é o desvio padrão intra-sujeito como descrito abaixo.

O parâmetro de não centralidade que corresponde ao limite superior equivalência é denotado como λ₂, e é dado por:

Sigma

O desvio padrão, σ, é calculado utilizando o coeficiente de variação (CV) intra-sujeito da seguinte maneira:

Notação

Termo	Descrição
α	nível de significância para o teste
ρ	razão da média da população de teste em relação à média da população de referência
δ1	limite de equivalência inferior
δ2	limite de equivalência superior
n	número de participantes em cada sequência. (Para os cálculos de poder, supõe-se que n é o mesmo para ambas as sequências).

Se você fornecer valores para poder e a diferença (ou razão), o Minitab calcula o tamanho amostral. O Minitab utiliza a fórmula de poder apropriada e um algoritmo iterativo para identificar o menor tamanho amostral n, para o qual o poder é maior ou igual ao valor especificado. O poder real para n tende a ser maior do que o poder especificado. Isto é porque n deve ser um número inteiro de valor discreto, e nenhum valor de n tende a produzir exatamente o valor de poder especificado.

Se você fornecer valores de poder e tamanho da amostra, o Minitab calcula os valores para a diferença. O Minitab utiliza a fórmula apropriada de poder e um algoritmo iterativo para identificar a diferença maior e/ou menor para a qual o poder é maior ou igual ao valor especificado.

Se você fornecer valores de poder e tamanho da amostra, o Minitab calcula os valores para a razão. O Minitab utiliza a fórmula apropriada de poder e um algoritmo iterativo para identificar a razão maior e/ou menor para a qual o poder é maior ou igual ao valor especificado.