Neste tópico
Poder para diferença
A primeira linha da saída indica como as hipóteses são especificadas para o teste de equivalência.
"Poder para diferença" indica que as hipóteses são especificadas em termos da diferença entre a média da população de teste e a média da população de referência (média de teste – média de referência).
Poder para razão
A primeira linha da saída indica como as hipóteses são especificadas para o teste de equivalência.
"Poder para razão" indica que as hipóteses são especificadas em termos da razão entre a média da população de teste e a média da população de referência por transformação logarítmica (média de teste / média de referência).
Hipótese nula e hipótese alternativa
- Hipótese nula
- O Minitab testa uma ou ambas as seguintes hipóteses nulas, dependendo da hipótese alternativa selecionada:
- A diferença (ou razão) entre a média da população de teste e a média da população de referência é maior ou igual ao limite superior de equivalência.
- A diferença (ou razão) entre a média da população de teste e a média da população de referência é menor ou igual ao limite inferior de equivalência.
- Hipótese alternativa
- A hipótese alternativa estabelece um ou ambos dos seguintes procedimentos:
- A diferença (ou razão) entre a média da população de teste e a média da população de referência é menor que o limite superior de equivalência.
- A diferença (ou razão) entre a média da população de teste e a média da população de referência é maior que limite inferior de equivalência.
Interpretação
Use as hipóteses nula e alternativa para se certificar que os critérios de equivalência estejam corretos e que você tenha selecionado a hipótese alternativa apropriada para testar.
Método
| Poder para a diferença: | Média de teste - média de referência |
|---|---|
| Hipótese nula: | Diferença ≤ -0,425 ou Diferença ≥ 0,425 |
| Hipótese alternativa: | -0,425 < Diferença < 0,425 |
| Nível α: | 0,05 |
Nestes resultados, o Minitab testa duas hipóteses nulas:
- A diferença entre a média da população de teste e a média da população de referência é menor ou igual ao limite inferior de equivalência de −0,425.
- A diferença entre a média da população de teste e a média da população de referência é maior ou igual ao limite superior de equivalência de 0,425.
α (alfa)
O nível de significância (indicado por alfa ou α) é o nível de risco máximo aceitável para rejeitar a hipótese nula quando ela é verdadeira (erro tipo I). Por exemplo, se você executar um teste de equivalência utilizando as hipóteses padrão, um α de 0,05 indica um risco de 5% de afirmar a equivalência quando a diferença entre a média de teste e a média de referência, a verdade, não estão dentro dos limites de equivalência.
O nível de α para um teste de equivalência também determina o nível de confiança para o intervalo de confiança. O nível de confiança é (1 - α) x 100% por padrão. Se você usar o método alternativo de cálculo do intervalo de confiança, o nível de confiança é (1 - 2α) x 100%.
Interpretação
Use o nível de significância para minimizar o valor do poder do teste quando a hipótese nula (H0) for verdadeira. Os valores mais elevados para o nível de significância dão mais poder ao teste, mas também aumentar a chance cometer um erro do tipo I, que está rejeitando a hipótese nula quando ela é verdadeira.
Desvio padrão intra-sujeito assumido
O desvio padrão intra-sujeito é o desvio padrão de múltiplos valores de resposta do mesmo participante. Esta medida de desvio padrão estima a magnitude do erro aleatório nas medidas de resposta de um mesmo participante depois de eliminar os efeitos do tratamento, efeitos de período e outros efeitos sistemáticos. Os valores mais altos indicam maior variabilidade nos valores de resposta de cada participante.
Interpretação
Se você realizar uma análise de poder para um teste de equivalência sobre a diferença, deve inserir o desvio padrão intra-sujeito. Este desvio padrão intra-sujeito assumido é uma estimativa do desvio padrão da população.
O Minitab utiliza o desvio padrão intra-sujeito assumido para a calcular o poder do teste. Os valores mais elevados do desvio padrão intra-sujeito indicam mais variação ou "ruído" nos dados, o que diminui o poder estatístico de um teste.
Coeficiente de variação intra-sujeito assumido
O coeficiente de variação intra-sujeito é o coeficiente de variação de valores múltiplos de resposta do mesmo participante. O coeficiente de variação é igual ao desvio padrão dividido pela média.
Esta variação da medida de desvio padrão estima a magnitude do erro aleatório nas medidas de resposta de um mesmo participante depois de eliminar os efeitos do tratamento, efeitos de período e outros efeitos sistemáticos. Os valores mais altos indicam maior variabilidade nos valores de resposta de cada participante.
Interpretação
Se você executar uma análise de poder para um teste de equivalência sobre a razão, deve inserir o coeficiente intra-sujeito de variação. Este coeficiente de variação intra-sujeito assumido é uma estimativa do coeficiente de variação da população.
O Minitab usa o coeficiente de variação intra-sujeirot assumido para calcular o poder do teste. Os valores mais elevados de coeficiente de variação intra-sujeito indicam mais variação ou "ruído" nos dados, o que diminui o poder estatístico de um teste.
Diferença
Este valor representa a diferença entre a média da população de teste e a média da população de referência.
Observação
As definições e interpretações neste tópico se aplicam a um teste de equivalência padrão que utilizam a hipótese alternativa padrão (Limite inferior < média de teste - média de referência < limite superior).
Interpretação
Se você inserir o tamanho amostral e o poder do teste, o Minitab calcula a diferença que o teste pode acomodar ao poder e tamanho de amostra especificados. Para amostras maiores, a diferença pode estar mais próxima de seus limites de equivalência.
Para investigar melhor a relação entre o tamanho da amostra e a diferença que o ensaio pode acomodar a um determinado poder, use a curva de poder.
Método
| Poder para a diferença: | Média de teste - média de referência |
|---|---|
| Hipótese nula: | Diferença ≤ -0,425 ou Diferença ≥ 0,425 |
| Hipótese alternativa: | -0,425 < Diferença < 0,425 |
| Nível α: | 0,05 |
Resultados
| Tamanho Amostral | Poder | Diferença |
|---|---|---|
| 4 | 0,9 | -0,278474 |
| 4 | 0,9 | 0,278474 |
| 8 | 0,9 | -0,329164 |
| 8 | 0,9 | 0,329164 |
| 12 | 0,9 | -0,348248 |
| 12 | 0,9 | 0,348248 |
Estes resultados mostram como o aumento do tamanho da amostra aumenta o tamanho da diferença que pode ser acomodadas a um determinado nível de poder:
- Com 4 participantes em cada sequência, o poder do teste é de pelo menos 0,9 quando a diferença fica aproximadamente entre −0,278 e 0,278.
- Com 8 participantes em cada sequência, o poder do teste é de pelo menos 0,9 quando a diferença fica aproximadamente entre −0,329 e 0,329.
- Com 12 participantes em cada sequência, o poder do teste é de pelo menos 0,9 quando a diferença fica aproximadamente entre −0,348 e 0,348.
Proporção
Este valor representa a razão da média da população de teste para a média da população de referência. Para realizar cálculos de poder para uma razão, você deve selecionar uma hipótese sobre Média de teste / média de referência (Razão, por transformação de log).
Observação
As definições e interpretação neste tópico se aplicam a um teste de equivalência que utiliza a hipótese alternativa padrão para a razão (Limite inferior < média de teste / média de referência < limite superior).
Interpretação
Se você digitar o tamanho amostral e o poder do teste, o Minitab calcula as razões mínimas e máximas que o teste pode acomodar no poder e tamanho de amostra especificado. Para amostras maiores, a razão pode estar mais próxima de seus limites de equivalência.
Para investigar melhor a relação entre o tamanho da amostra e as razões que o ensaio pode acomodar a um determinado poder, use a curva de poder.
Método
| Poder para razão: | Média de teste/média de referência |
|---|---|
| Hipótese nula: | Razão ≤ 0,9 ou Razão ≥ 1,1 |
| Hipótese alternativa: | 0,9 < Razão < 1,1 |
| Nível α: | 0,05 |
Resultados
| Tamanho Amostral | Poder | Razão |
|---|---|---|
| 10 | 0,9 | 0,91749 |
| 10 | 0,9 | 1,07903 |
| 20 | 0,9 | 0,91207 |
| 20 | 0,9 | 1,08544 |
Estes resultados mostram como o aumento do tamanho amostral aumenta a o intervalo de razões que o ensaio pode acomodar a um determinado nível de poder:
- Com 10 observações em cada sequência, o poder do teste é de pelo menos 0,9 quando a razão fica aproximadamente entre 0,92 e 1,08.
- Com 20 observações em cada sequência, o poder do teste é de pelo menos 0,9 quando a razão fica aproximadamente entre 0,91 e 1,09.
Tamanho amostral
O tamanho amostral é o número total de observações na amostra. Para um estudo cruzado 2x2, o tamanho amostral se refere ao número de participantes em cada sequência do estudo.
Interpretação
Use o tamanho amostral para estimar quantas observações são necessárias para obter um certo valor de poder para o teste de equivalência a uma diferença específica.
Se você inserir uma diferença (ou razão) e um valor de poder para o teste, o Minitab calcula o tamanho que sua amostra deve ter. Como os tamanhos amostrais são números inteiros, o poder real do teste pode ser um pouco maior do que o valor de poder que você especificar.
Se você aumentar o tamanho amostral, o poder do teste também aumentará. Você quer observações suficientes na sua amostra para alcançar o poder adequado. Porém, você não quer um tamanho amostral tão grande a ponto de perder tempo e dinheiro em amostragens desnecessárias ou detectar diferenças sem importância para serem estatisticamente significativas.
Para investigar melhor a relação entre o tamanho amostral e a diferença (ou razão) que o ensaio pode acomodar a um determinado poder, use a curva de poder.
Método
| Poder para a diferença: | Média de teste - média de referência |
|---|---|
| Hipótese nula: | Diferença ≤ -0,425 ou Diferença ≥ 0,425 |
| Hipótese alternativa: | -0,425 < Diferença < 0,425 |
| Nível α: | 0,05 |
Resultados
| Diferença | Tamanho Amostral | Poder Alvo | Poder Real |
|---|---|---|---|
| 0,0 | 2 | 0,9 | 0,978589 |
| 0,1 | 2 | 0,9 | 0,931544 |
| 0,2 | 3 | 0,9 | 0,972795 |
| 0,3 | 6 | 0,9 | 0,943646 |
| 0,4 | 107 | 0,9 | 0,900500 |
Estes resultados mostram que, conforme o tamanho da diferença aumenta e se aproxima do valor do limite de equivalência, é necessário um maior número de amostras para alcançar um determinado poder. Se a diferença é de 0,1, você precisa apenas de 2 participantes de cada sequência para alcançar um poder de 0,9. Se a diferença é de 0,4, você precisa de pelo menos 107 participantes em cada sequência para alcançar um poder de 0,9.
Poder
O poder de um teste de equivalência é a probabilidade de que o teste demonstre que a diferença está dentro de seus limites de equivalência, quando ela realmente está. O poder de um teste de equivalência é afetado pelo tamanho amostral, a diferença, os limites de equivalência, a variabilidade dos dados e o nível de significância do teste.
Para obter mais informações, vá para Poder para testes de equivalência.
Interpretação
Se você inserir um tamanho amostral e uma diferença (ou taxa), o Minitab calcula o poder do teste. Em geral, um valor de poder de pelo menos 0,9 é considerado adequado. Um poder de 0,9 indica que você tem uma probabilidade de 90% de demonstrar a equivalência quando a diferença (ou proporção) entre as médias de população está, na verdade, dentro dos limites de equivalência. Se um teste de equivalência tem baixo poder, você pode deixar de demonstrar a equivalência, mesmo quando a média de teste e a média de referência são equivalentes.
Normalmente, quando o tamanho amostral é menor ou quando a diferença (ou proporção) está mais perto de um limite de equivalência, o teste tem menos poder para afirmar equivalência.
Método
| Poder para a diferença: | Média de teste - média de referência |
|---|---|
| Hipótese nula: | Diferença ≤ -0,425 ou Diferença ≥ 0,425 |
| Hipótese alternativa: | -0,425 < Diferença < 0,425 |
| Nível α: | 0,05 |
Resultados
| Diferença | Tamanho Amostral | Poder |
|---|---|---|
| 0,3 | 8 | 0,984946 |
| 0,3 | 12 | 0,999089 |
| 0,4 | 8 | 0,189487 |
| 0,4 | 12 | 0,244815 |
Nestes resultados, para uma diferença de 0,3, o poder do teste é de cerca de 0,98, com um tamanho amostral de 8, 0,99 e com um tamanho amostral 15. Para uma diferença de 0,4, o poder é de aproximadamente 0,19, com um tamanho amostral de 8, e 0,24 com um tamanho amostral de 12.
Curva de poder
A curva de poder representa graficamente o poder do teste versus a diferença entre a média de teste e a média de referência.
Interpretação
Use a curva de poder para avaliar o tamanho amostral ou o poder adequado para o seu teste.
A curva de poder representa todas as combinações de poder e diferença (ou razão) para cada tamanho amostral quando o nível de significância e o desvio padrão (ou coeficiente de variação) são mantidos constantes. Cada símbolo na curva de poder representa um valor calculado com base nos valores inseridos. Por exemplo, se você inserir um tamanho amostral e um valor de poder, o Minitab calcula a diferença (ou razão) correspondente e exibe o valor calculado no gráfico.
Examine os valores na curva para determinar a diferença (ou razão) entre a média de teste e a média de referência que pode ser acomodada a um determinado valor de poder e tamanho amostral. Em geral, um valor de poder de 0,9 é considerado adequado. No entanto, alguns profissionais consideram o valor de poder de 0,8 como adequado. Se um teste de equivalência tiver baixo poder, talvez não seja possível demonstrar a equivalência mesmo se as médias da população forem equivalentes. Se você aumentar o tamanho amostral, o poder do teste também aumentará. Você quer observações suficientes na sua amostra para alcançar o poder adequado. Porém, você não quer um tamanho amostral tão grande a ponto de perder tempo e dinheiro em amostragens desnecessárias ou detectar diferenças sem importância para serem estatisticamente significativas. Normalmente, as diferenças (ou razões) que estão mais próximas aos limites de equivalência exigem mais poder para demonstrar a equivalência.
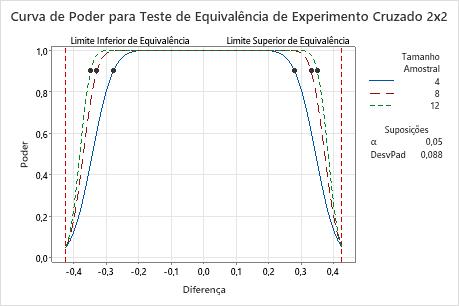
Neste gráfico, as curvas de poder para todos os tamanhos das amostras mostram que o ensaio tem potência adequada (≥ 0,9) para uma diferença de aproximadamente ± 0,25. Os tamanhos de amostra se referem ao número de participantes em cada sequência. A curva de poder para um tamanho de amostra de 4 mostra que o teste tem um poder de 0,9 para uma diferença aproximada de ± 0,28. A curva de poder de um tamanho de amostra de 12 mostra que o teste tem um poder de 0,9 para uma diferença aproximada de ±0,33. Observe que o aumento do tamanho da amostra para 12 aumenta, apenas muito ligeiramente, a diferença que pode ser acomodada a um poder de 0,9. Para cada curva, como a diferença se aproxima do limite de equivalência inferior ou superior do limite de equivalência, o poder do teste diminui e se aproxima de α (alfa, que é o risco de afirmar a equivalência quando ela não é verdadeira).
