Um engenheiro de qualidade em uma empresa de saúde do consumidor quer determinar se o seu antiácido genérico equivale a um antiácido de marca. Dois grupos de participantes recebem um ciclo de 5 dias de um antiácido, seguido por um período de limpeza de 2 semanas e depois um ciclo de 5 dias do outro antiácido. O grupo 1 recebe o antiácido genérico (o tratamento de teste) seguido pelo antiácido de marca (o tratamento de referência). O grupo 2 recebe o antiácido de marca seguido pelo antiácido genérico. O engenheiro mede o pH gástrico no último dia de cada tratamento. Como valores de pH menores representam mais acidez, valores mais altos significam que o fármaco é mais eficaz. O engenheiro considerará os antiácidos equivalentes se o pH de teste ficar em 10% do pH de referência.
O engenheiro realiza um teste de equivalência de um experimento cruzado 2x2 para determinar se o pH de teste e de referência são equivalentes. O intervalo de confiança para a diferença não está completamente dentro do intervalo de equivalência (-0,425, 0,425). Por isso, o engenheiro não pode alegar uma equivalência entre os antiácidos. Para melhorar o experimento para o próximo estudo, o engenheiro usa um cálculo de poder e tamanho de amostra para estimar o tamanho de amostra necessário para se obter um poder de 90% (0,9) para o teste. A partir de amostras anteriores, o engenheiro estima o desvio padrão dentro do sujeito da população é de 0,088.
- Selecione .
- Em Hipótese sobre, selecione Média de teste - média de referência (Diferença).
- Em O que você deseja determinar? (Hipótese alternativa), selecione Limite inferior < média de teste - média de referência < limite superior.
- Em Limite inferior, insira -0,425. Em Limite superior, insira 0,425.
- Em Diferenças (dentro dos limites), insira 0,1 0,2 0,3 0,4.
- Em Valores de poder, insira 0,9.
- Em Desvio padrão dentro dos indivíduos, insira 0,088.
- Clique em OK.
Interpretar os resultados
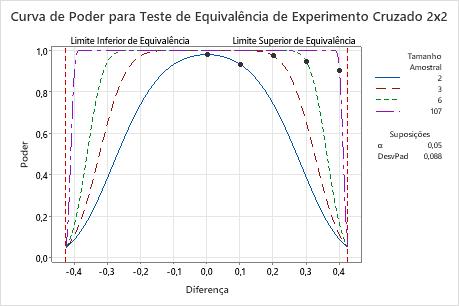
Se a diferença for de 0,1, o engenheiro precisa apenas 2 participantes em cada sequência para alcançar um poder de pelo menos 0,9 (um poder real é de aproximadamente 0,93).
Quando a diferença está mais próxima do limite de equivalência superior (0,425), o engenheiro precisa de mais observações para alcançar o mesmo poder. Por exemplo, para uma diferença de 0,4, o engenheiro precisa, pelo menos, de 107 participantes em cada sequência para alcançar um poder de 0,9.
Para qualquer amostra, como a diferença se aproxima do limite de equivalência inferior ou do limite de equivalência superior, o poder do teste diminui e se aproxima de α (alfa, que é o risco de afirmar a equivalência quando não ela não é verdadeira).
Método
| Poder para a diferença: | Média de teste - média de referência |
|---|---|
| Hipótese nula: | Diferença ≤ -0,425 ou Diferença ≥ 0,425 |
| Hipótese alternativa: | -0,425 < Diferença < 0,425 |
| Nível α: | 0,05 |
Resultados
| Diferença | Tamanho Amostral | Poder Alvo | Poder Real |
|---|---|---|---|
| 0,0 | 2 | 0,9 | 0,978589 |
| 0,1 | 2 | 0,9 | 0,931544 |
| 0,2 | 3 | 0,9 | 0,972795 |
| 0,3 | 6 | 0,9 | 0,943646 |
| 0,4 | 107 | 0,9 | 0,900500 |