Um analista qualidade quer determinar se a quantidade média de ingrediente ativo em um tipo genérico de analgésico está dentro de 1 mg da quantidade média de um tipo popular de analgésico. Antes de coletar os dados para um teste de equivalência para 2 amostras, o analista usa um cálculo de poder e tamanho de amostra para determinar o tamanho que a amostra deve ter para obter um poder de 90% (0,9). A partir das amostras anteriores, o analista estima que o desvio padrão da população é 0,41.
- Selecione .
- Em Hipótese sobre, selecione Média de teste - média de referência (Diferença).
- Em O que você deseja determinar? (Hipótese alternativa), selecione Limite inferior < média de teste - média de referência < limite superior.
- Em Limite inferior, insira -1. Em Limite superior, insira 1.
- Em Diferenças (dentro dos limites), insira 0,025.
- Em Valores de poder, insira 0,9.
- Em Desvio padrão, insira 0,41.
- Clique em OK.
Interpretar os resultados
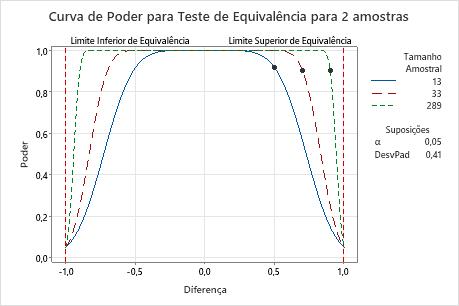
Se a diferença for de 0,5, o analista precisa de 13 observações em cada grupo para obter um poder de pelo menos 0,9. Se o analista utiliza um tamanho amostral de 13, o poder do teste é de aproximadamente 0,92.
Quando a diferença está mais próxima do limite inferior da equivalência (-1) ou o limite superior de equivalência (1), o analista necessita de uma amostra maior para alcançar o mesmo poder. Por exemplo, para uma diferença de 0,9, o analista precisa de um tamanho amostral de pelo menos 289 observações em cada grupo para obter um poder de 0,9.
Para qualquer amostra, conforme a diferença se aproxima do limite de equivalência inferior ou do limite de equivalência superior, o poder do teste diminui e se aproxima de α (alfa, que é o risco de afirmar a equivalência quando não ela não é verdadeira).
Método
| Poder para a diferença: | Média de teste - média de referência |
|---|---|
| Hipótese nula: | Diferença ≤ -1 ou Diferença ≥ 1 |
| Hipótese alternativa: | -1 < Diferença < 1 |
| Nível α: | 0,05 |
| Desvio padrão assumido: | 0,41 |
Resultados
| Diferença | Tamanho Amostral | Poder Alvo | Poder Real |
|---|---|---|---|
| 0,5 | 13 | 0,9 | 0,915407 |
| 0,7 | 33 | 0,9 | 0,902461 |
| 0,9 | 289 | 0,9 | 0,900360 |