Neste tópico
Poder para diferença
A primeira linha da saída indica como as hipóteses são especificadas para o teste de equivalência.
"Poder para diferença" indica que as hipóteses são especificadas em termos de diferença entre a média da população de teste e o valor alvo (média de Teste - alvo).
Hipótese nula e hipótese alternativa
- Hipótese nula
- O Minitab testa uma ou ambas as seguintes hipóteses nulas, dependendo da hipótese alternativa selecionada:
- A diferença entre a média da população e o alvo é maior ou igual ao limite superior de equivalência.
- A diferença entre a média da população e o alvo é menor ou igual ao limite inferior de equivalência.
- Hipótese alternativa
- A hipótese alternativa afirma uma ou ambas as seguintes:
- A diferença entre a média da população e o alvo é menor ou igual ao limite superior de equivalência.
- A diferença entre a média da população e o alvo é maior do que limite inferior de equivalência.
Interpretação
Use as hipóteses nula e alternativa para se certificar que os critérios de equivalência estejam corretos e que você tenha selecionado a hipótese alternativa apropriada para testar.
Método
| Poder para a diferença: | Média de teste - alvo |
|---|---|
| Hipótese nula: | Diferença ≤ -0,42 ou Diferença ≥ 0,42 |
| Hipótese alternativa: | -0,42 < Diferença < 0,42 |
| Nível α: | 0,05 |
| Desvio padrão assumido: | 0,332 |
- A diferença entre a média da população de teste e o alvo é menor ou igual ao limite inferior de equivalência de −0,42.
- A diferença entre a média da população de teste e o alvo é maior ou igual ao limite superior de equivalência de 0,42.
α (alfa)
O nível de significância (indicado por alfa ou α) é o nível máximo aceitável de risco para rejeitar a hipótese nula quando ela é verdadeira (erro tipo I). Por exemplo, se você realizar um teste de equivalência utilizando as hipóteses padrão, um α de 0,05 indica um risco de 5% de afirmar equivalência quando a diferença entre a média e o alvo, na verdade, não está dentro dos limites de equivalência.
O nível de α para um teste de equivalência também determina o nível de confiança para o intervalo de confiança. O nível de confiança é de 1 - α por padrão, ou 1 - 2a se você usar o método alternativo de cálculo do intervalo de confiança.
Interpretação
Use o nível de significância para minimizar o valor do poder do teste quando a hipótese nula (H0) for verdadeira. Os valores mais elevados para o nível de significância dão mais poder ao teste, mas também aumentar a chance cometer um erro do tipo I, que está rejeitando a hipótese nula quando ela é verdadeira.
Desvio padrão suposto
O desvio padrão é a medida mais comum da dispersão, ou quanto os dados variam em relação à média. A variação que é aleatória ou natural de um processo é frequentemente referida como ruído.
Interpretação
O desvio padrão suposto é um planejamento estimado do desvio padrão da população que você insere para a análise de poder. O Minitab utiliza o desvio padrão suposto a calcular o poder do teste. Os valores mais elevados do desvio padrão indicam que existe mais variação nos dados, o que diminui o poder estatístico de um teste.Diferença
Este valor representa a diferença entre a média da população e o alvo.
Observação
As definições e interpretações neste tópico se aplicam a um teste de equivalência padrão que utilizam a hipótese alternativa padrão (Limite inferior < média de teste - alvo < limite superior).
Interpretação
Se você inserir o tamanho amostral e o poder do teste, o Minitab calcula a diferença que o teste pode acomodar ao poder e tamanho de amostra especificados. Para amostras maiores, a diferença pode estar mais próxima de seus limites de equivalência.
Para investigar melhor a relação entre o tamanho da amostra e a diferença que o ensaio pode acomodar a um determinado poder, use a curva de poder.
Método
| Poder para a diferença: | Média de teste - alvo |
|---|---|
| Hipótese nula: | Diferença ≤ -0,42 ou Diferença ≥ 0,42 |
| Hipótese alternativa: | -0,42 < Diferença < 0,42 |
| Nível α: | 0,05 |
| Desvio padrão assumido: | 0,732 |
Resultados
| Tamanho Amostral | Poder | Diferença |
|---|---|---|
| 30 | 0,9 | * |
| 40 | 0,9 | -0,071272 |
| 40 | 0,9 | 0,071272 |
| 60 | 0,9 | -0,140212 |
| 60 | 0,9 | 0,140212 |
| 100 | 0,9 | -0,204306 |
| 100 | 0,9 | 0,204306 |
Estes resultados mostram como o aumento do tamanho da amostra aumenta o tamanho da diferença que pode ser acomodadas a um determinado nível de poder:
- Com 30 observações, não é possível atingir um poder de 0,9 para afirmar a equivalência, independentemente da diferença.
- Com 40 pares de observações, o poder do teste é de pelo menos 0,9 quando a diferença é fica aproximadamente entre −0,07 e 0,07.
- Com 60 pares de observações, o poder do teste é de pelo menos 0,9 quando a diferença é fica aproximadamente entre −0,14 e 0,14.
- Com 100 pares de observações, o poder do teste é de pelo menos 0,9 quando a diferença é fica aproximadamente entre −0,20 e 0,20.
Tamanho amostral
O tamanho amostral é o número total de observações na amostra.
Interpretação
Use o tamanho amostral para estimar quantas observações são necessárias para obter um certo valor de poder para o teste de equivalência a uma diferença específica.
Se você inserir a diferença e um valor de poder para o teste, o Minitab calcula o tamanho que sua amostra deve ter.Como os tamanhos amostrais são números inteiros, o poder real do teste pode ser um pouco maior do que o valor de poder que você especificar.
Se você aumentar o tamanho amostral, o poder do teste também aumentará. Você quer observações suficientes na sua amostra para alcançar o poder adequado. Porém, você não quer um tamanho amostral tão grande a ponto de perder tempo e dinheiro em amostragens desnecessárias ou detectar diferenças sem importância para serem estatisticamente significativas.
Para investigar melhor a relação entre o tamanho da amostra e a diferença que o ensaio pode acomodar a um determinado poder, use a curva de poder.
Método
| Poder para a diferença: | Média de teste - alvo |
|---|---|
| Hipótese nula: | Diferença ≤ -0,42 ou Diferença ≥ 0,42 |
| Hipótese alternativa: | -0,42 < Diferença < 0,42 |
| Nível α: | 0,05 |
| Desvio padrão assumido: | 0,732 |
Resultados
| Diferença | Tamanho Amostral | Poder Alvo | Poder Real |
|---|---|---|---|
| 0,1 | 47 | 0,9 | 0,903687 |
| 0,2 | 97 | 0,9 | 0,902206 |
| 0,3 | 321 | 0,9 | 0,900788 |
Estes resultados mostram que, como o tamanho da diferença aumenta e se aproxima do valor do limite de equivalência, é necessário um maior tamanho amostral para alcançar um determinado poder. Se a diferença for de 0,1, você precisa de pelo menos 47 observações para alcançar um poder de 0,9. Se a diferença for de 0,3, você precisa de pelo menos 321 observações para alcançar um poder de 0,9.
Poder
Observação
As definições e interpretações neste tópico se aplicam a um teste de equivalência padrão que utilizam a hipótese alternativa padrão (Limite inferior < média de teste - alvo < limite superior).
O poder de um teste de equivalência é a probabilidade de que o teste demonstre que a diferença está dentro de seus limites de equivalência, quando ela realmente está. O poder de um teste de equivalência é afetado pelo tamanho amostral, a diferença, os limites de equivalência, a variabilidade dos dados e o nível de significância do teste.
Para obter mais informações, vá para Poder para testes de equivalência.
Interpretação
Se você inserir um tamanho amostral e uma diferença, o Minitab calcula o poder do teste. Em geral, um valor de poder de 0,9 é considerado adequado. Um poder de 0,9 indica que você tem uma probabilidade de 90% de demonstrar a equivalência quando a diferença da população está, na verdade, dentro dos limites de equivalência. Se um teste de equivalência tem baixo poder, você pode deixar de demonstrar a equivalência, mesmo quando a média da população e o alvo são equivalentes.
Se você inserir a diferença e um valor de poder para o teste, o Minitab calcula o tamanho que sua amostra deve ter. O Minitab também calcula o poder real do teste para aquele tamanho da amostral. Como os tamanhos amostrais são números inteiros, o poder real do teste pode ser um pouco maior do que o valor de poder que você especificar.
Normalmente, quando o tamanho amostral é menor ou a diferença está mais perto de um limite de equivalência, o teste tem menos poder para afirmar equivalência.
Método
| Poder para a diferença: | Média de teste - alvo |
|---|---|
| Hipótese nula: | Diferença ≤ -0,42 ou Diferença ≥ 0,42 |
| Hipótese alternativa: | -0,42 < Diferença < 0,42 |
| Nível α: | 0,05 |
| Desvio padrão assumido: | 0,732 |
Resultados
| Diferença | Tamanho Amostral | Poder |
|---|---|---|
| 0,1 | 20 | 0,516387 |
| 0,1 | 35 | 0,806390 |
| 0,2 | 20 | 0,341093 |
| 0,2 | 35 | 0,538352 |
Nestes resultados, para uma diferença de 0,1, o poder do teste é de cerca de 0,52, com um tamanho amostral de 20, 0,81 e com um tamanho amostral 35. Para uma diferença de 0,2, o poder é de aproximadamente 0,34, com um tamanho amostral de 20, e 0,54 com um tamanho amostral de 35.
Curva de poder
A curva de poder representa graficamente o poder do teste versus a diferença entre a média de teste e a média de referência e o alvo.
Interpretação
Use a curva de poder para avaliar o tamanho amostral ou o poder adequado para o seu teste.
A curva de poder representa todas as combinações de poder e diferença para cada tamanho amostral, quando o nível de significância e o desvio padrão são mantidos constantes. Cada símbolo na curva da poder representa um valor calculado com base nos valores inseridos. Por exemplo, se você inserir um tamanho amostral e um valor de poder, o Minitab calcula a diferença correspondente e exibe o valor calculado no gráfico.
Examine os valores na curva para determinar a diferença entre a média e o alvo que pode ser acomodada a um determinado valor de poder e tamanho amostral. Em geral, um valor de poder de 0,9 é considerado adequado. No entanto, alguns profissionais consideram o valor de poder de 0,8 como adequado. Se um teste de equivalência tiver baixo poder, talvez não seja possível demonstrar a equivalência mesmo se a média for equivalente ao alvo. Se você aumentar o tamanho amostral, o poder do teste também aumentará. Você quer observações suficientes na sua amostra para alcançar o poder adequado. Porém, você não quer um tamanho amostral tão grande a ponto de perder tempo e dinheiro em amostragens desnecessárias ou detectar diferenças sem importância para serem estatisticamente significativas. Normalmente, as diferenças que estão mais próximas aos limites de equivalência exigem mais poder para demonstrar a equivalência.
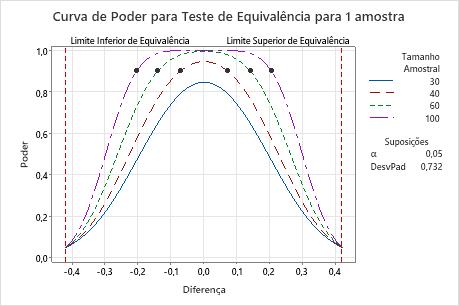
Neste gráfico, a curva de poder para um tamanho amostral de 30 mostra que o teste não pode alcançar um poder de 0,9 por nenhuma diferença de tamanho. A curva de poder para um tamanho amostral de 40 mostra que o teste tem poder de 0,9 para uma diferença de aproximadamente 0,0. A curva de poder de um tamanho amostral de 100 mostra que o teste tem um poder de 0,9 para uma diferença de aproximadamente ± 0,2. Para cada curva, como a diferença se aproxima do limite de equivalência inferior ou do limite de equivalência superior, o poder do teste diminui e se aproxima de α (alfa, que é o risco de afirmar a equivalência quando não ela não é verdadeira).
