Classificação da média
- Classifica as amostras combinadas, atribui à menor observação uma classificação de 1, à segunda menor observação uma classificação de 2, e assim por diante.
- Se duas ou mais observações estão empatadas, o Minitab atribui a classificação média a ambas as observações.
- Calcula a média das classificações de cada amostra.
O Minitab exibe os valores para cada grupo na classificação da média na saída.
Valor Z
Fórmula
O Minitab calcula o valor-z para cada grupo da seguinte maneira:
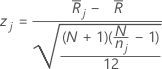
Notação
| Termo | Descrição |
|---|---|
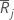 | classificação média para o grupo j |
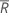 | classificação média para todas as observações |
| N | número de observações |
| nj | número de observações para o jo grupo |
Classificação de valores empatados
- Organiza as observações em ordem crescente.
- Atribui classificações a cada observação como se não houvesse nenhum vínculo.
- Para um conjunto empatado, pegue a média das classificações correspondentes e atribua esse valor como a novo classificação para cada valor empatado nesse conjunto.
Exemplo
Uma amostra tem 9 observações: 2,4, 5,3, 2,4, 4,0, 1,2, 3,6, 4,0, 4,3 e 4,0
| Observação | Classificação (assumindo que não há empate) | Atribuir postos |
|---|---|---|
| 1,2 | 1 | 1 |
| 2,4 | 2 | 2,5 |
| 2,4 | 3 | 2,5 |
| 3,6 | 4 | 4 |
| 4,0 | 5 | 6 |
| 4,0 | 6 | 6 |
| 4,0 | 7 | 6 |
| 4,3 | 8 | 8 |
| 5,3 | 9 | 9 |
- O número de conjuntos de empates = 2
- O número de valores empatados no primeiro conjunto = 2
- O número de valores empatados no segundo conjunto = 3
H
Fórmula

Sob a hipótese nula, a distribuição do qui-quadrado com k - 1 graus de liberdade se aproxima da distribuição de H. A aproximação é razoavelmente precisa, quando nenhum grupo tem menos de cinco observações. Um valor mais elevado de H fornece evidência mais forte para a hipótese nula de que a diferença entre algumas das medianas é estatisticamente significativa.
Alguns autores como Lehmann (1975)1, sugerem o ajuste de H quando os dados têm empates. O Minitab exibe H(adj) quando os dados têm empates.
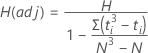
Sob a hipótese nula, a distribuição do qui-quadrado com k - 1 graus de liberdade se aproxima da distribuição de H e H(adj).
Valor de p = 1 – CDF (χ2H, df)
Valor de p = 1 – CDF (χ2H(adj), df)
Para amostras pequenas, o Minitab recomenda que você use tabelas exatas. Para obter mais detalhes, consulte Hollander e Wolfe (1973)2.
Notação
| Termo | Descrição |
|---|---|
| nj | número de observações no grupo j |
| N | tamanho total da amostra |
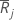 | média de classificações do grupo j |
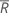 | média de todas as classificações |
| ti | número de valores empatados no io conjunto de empates |
