S
A estatística de teste tem uma distribuição de qui-quadrado ( χ2) aproximada, com graus de liberdade associados (k – 1). Se os dados dentro de um ou mais blocos tiverem empates, o Minitab usa a classificação média e imprime um teste estatístico que foi corrigido para empates. Para obter mais informações sobre este método, consulte M. Hollander e D.A. Wolfe (1973)1.
Fórmula
Para calcular a estatística de teste de qui-quadrado, o Minitab classifica os dados separadamente dentro de cada bloco e soma as classificações para cada tratamento.
Se os dados não têm empates, a fórmula é:
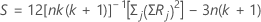
Se os dados têm empates:

em que C é um fator de correção que é igual a:
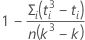
Notação
| Termo | Descrição |
|---|---|
| j | 1, 2, ..., k |
| k | o número de condições de tratamento |
| n | o número de blocos |
| Rj | a soma das classificações para o tratamento j |
| ii | 1, 2, ..., m |
| m | o número de conjuntos de empates |
| ti | O número de pontuações empatadas no ioconjunto de empates |
- M. Hollander e D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc.
Mediana global
Para entender como calcular os efeitos do tratamento, as medianas de bloco, e a mediana global, considere os dados a seguir.
| Bloco | ||||
| Tratamento | 1 | 2 | 3 | 4 |
| 1 | 0,15 | 0,26 | 0,23 | 0,99 |
| 2 | 0,55 | 0,26 | −0,22 | 0,99 |
| 3 | 0,55 | 0,66 | 0,77 | 0,99 |
Para calcular os efeitos (pelo método de Doksum1), primeiramente, encontre a diferença média entre os pares de tratamentos. As diferenças pareadas para o tratamento 1 menos o tratamento 2 são 0,15 - 0,55 = - 0,4, 0,26 -0,26 = 0, 0,23 - (-0,22) = 0,45, e 0,99 - 0,99 = 0. A mediana das diferenças é 0. Executar este cálculo para os outros dois pares resulta -0,4 para o tratamento 1 menos o tratamento 3, e -0,2 para o tratamento 2 menos o tratamento 3.
O efeito de cada tratamento é a média das diferenças medianas daquele tratamento com todos os outros tratamentos (incluindo ele próprio). Para os dados apresentados neste exemplo, efeito (2) = [mediana (2 - 1) + mediana (2 - 2) + mediana (2 - 3)] / 3 = (0,00 + 0,00 - 0,20) / 3 = -0,0667. Da mesma forma, o efeito de (1) = -0,1333 e de efeito (3) = 0,20.
Para calcular as medianas de bloco ajustadas, ajuste cada observação subtraindo o efeito do tratamento apropriado da observação. As medianas de bloco ajustadas são simplesmente as medianas desses dados ajustadas e calculadas dentro de cada bloco. A mediana global é a mediana das medianas de bloco ajustadas. A mediana estimada para cada nível de tratamento é o efeito do tratamento somada à mediana global.
- M. Hollander and D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc., pp. 158 – 161.
Classificação de valores empatados
- Organiza as observações em ordem crescente.
- Atribui classificações a cada observação como se não houvesse nenhum vínculo.
- Para um conjunto empatado, pegue a média das classificações correspondentes e atribua esse valor como a novo classificação para cada valor empatado nesse conjunto.
Exemplo
Uma amostra tem 9 observações: 2,4, 5,3, 2,4, 4,0, 1,2, 3,6, 4,0, 4,3 e 4,0
| Observação | Classificação (assumindo que não há empate) | Atribuir postos |
|---|---|---|
| 1,2 | 1 | 1 |
| 2,4 | 2 | 2,5 |
| 2,4 | 3 | 2,5 |
| 3,6 | 4 | 4 |
| 4,0 | 5 | 6 |
| 4,0 | 6 | 6 |
| 4,0 | 7 | 6 |
| 4,3 | 8 | 8 |
| 5,3 | 9 | 9 |
- O número de conjuntos de empates = 2
- O número de valores empatados no primeiro conjunto = 2
- O número de valores empatados no segundo conjunto = 3
