Métodos e fórmulas para Teste de Wilcoxon para 1 amostra

Selecione o método ou a fórmula de sua escolha.

Neste tópico

Médias pareadas
Mediana Estimada
Estatística de Wilcoxon
Valor de p
Intervalo de confiança

Médias pareadas

Médias pareadas (também chamadas médias de Walsh) são as médias de cada par de valores possíveis no conjunto de dados, incluindo o próprio par de cada valor.

Fórmula

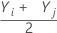= todas as médias pareadas para i ≤ j.

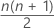= o número total de médias pareadas

Notação

Termo	Descrição
Y_i	i^o valor no conjunto de dados
Y_j	j^o valor no conjunto de dados
n	tamanho médio

Mediana Estimada

Permita que W_{( 1 )}< W_{( 2 )}< ... < W_{( M )} denote os valores ordenados de médias pareadas (também chamadas médias de Walsh), em que M = n(n+1)/2. Se M for ímpar, a mediana estimada é o valor do meio. Se M for par, a mediana estimada é a média dos dois valores do meio. O Minitab obtém a estimativa do ponto da mediana da população usando um algoritmo baseado em Johnson e Mizoguchi (1978)¹.

D.B. Johnson and T. Mizoguchi (1978). "Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm," SIAM Journal of Computing 7, pp.147-153.

Estatística de Wilcoxon

A estatística de Wilcoxon é o número de pares de médias (também chamadas médias de Walsh) que são maiores do que a mediana hipotética, além de uma metade do número de pares de médias que são iguais à mediana hipotética. A estatística de Wilcoxon é denotada como W. O Minitab obtém a estatística de teste usando um algoritmo baseado em Johnson e Miizoguchi (1978)¹.

D.B. Johnson e T. Mizoguchi (1978). "Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm," SIAM Journal of Computing 7, 147-153.

Valor de p

O teste estatístico de Wilcoxon, W, é a soma das classificações associadas às observações que excedem a mediana hipotética. O Minitab calcula a estatística de teste utilizando médias pareadas (Walsh), conforme descrito em Johnson e Mizoguchi¹:

O número de observações, N, é reduzido em um para cada observação que é igual à mediana hipotética. O tamanho da amostra resultante é n.
Excluir observações que são iguais à mediana hipotética. Calcular n(n + 1) / 2 médias de Walsh pareadas (Y_i + Y_j) / 2 para i ≤ j de observações.

Para os tamanhos de amostra grandes, a distribuição de W é aproximadamente normal. Especificamente:

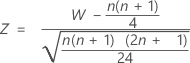é aproximadamente distribuído como uma distribuição normal com uma média de 0 e um desvio padrão de 1, N(0,1).

O valor de p com aproximação normal para as três hipóteses alternativas usa uma correção de continuidade de 0,5.

Hipótese alternativa	Valor de p
H₁: Mediana > mediana hipotética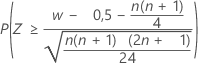
H₁: Mediana < mediana hipotética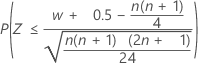
H₁: Mediana ≠ mediana hipotética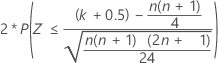

Notação

Termo	Descrição
n	o número de pontos de dados observados após as observações que são iguais ao valor mediano hipotético são omitidos
W	o teste estatístico de Wilcoxon
w	o número médias de Walsh que excedem à mediana hipotética, além de uma metade do número de médias de Walsh que são iguais à mediana hipotética.
k

D.B. Johnson and T. Mizoguchi (1978). "Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm," SIAM Journal of Computing 7, pp.147-153.

Intervalo de confiança

O intervalo de confiança é o conjunto de valores (d) para o qual o teste de H₀: mediana = d não é rejeitada em favor de H₁: mediana ≠ d, usando o nível de confiança (α = 1 - (confiança percentual) / 100). O teste de Wilcoxon para 1 amostra nem sempre alcança o nível de confiança especificado porque a estatística de Wilcoxon é discreta. Por essa razão, o Minitab usa uma aproximação normal com uma correção de continuidade para calcular o nível de confiança mais próximo possível.