Exemplo de Teste de equivalência com dados pareados

Um engenheiro de uma empresa de cuidados com os olhos testa uma nova solução de limpeza para lentes de contato. O engenheiro quer verificar se a nova solução limpa as lentes, assim como a marca líder. O engenheiro faz um teste com 14 participantes usando lentes de contato por um dia e depois limpando essas lentes. Cada participante limpa uma lente com a nova solução e a outra com a marca líder. O engenheiro avalia a limpeza de cada lente medindo o ângulo de contato de uma gota de fluido na lente. O ângulo de contato é afetado por película ou depósitos nas lentes. Para ser equivalente, o ângulo médio para a nova solução deve estar dentro de ± 0,5 graus do ângulo médio da marca líder.

O engenheiro realiza um teste de equivalência com dados pareados para determinar se as duas soluções são equivalentes.

Abra os dados amostrais, LimpadorLentesContato.MWX.
Selecione Estat > Testes de equivalência > Pareado.
Em Amostra de teste, insira Nova.
Em Amostra de referência, insira Marca Líder.
Em Hipótese sobre, selecione Média de teste - média de referência.
Em O que você deseja determinar? (Hipótese alternativa), selecione Limite inferior < média de teste - média de referência < limite superior.
Em Limite inferior, insira -0,5.
Em Limite superior, insira 0,5.
Clique em OK.

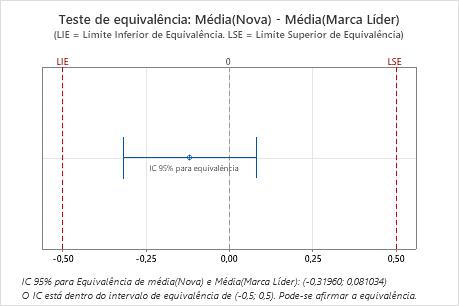
Interpretar os resultados

Como o intervalo de confiança fica completamente dentro do intervalo de equivalência, o engenheiro conclui que as duas soluções de limpeza são equivalentes.

Variável	N	Média	DesvPad	EP Média
Nova	14	88,604	1,5578	0,41634
Marca Líder	14	88,724	1,5907	0,42514

Hipótese nula:	Diferença ≤ -0,5 ou Diferença ≥ 0,5
Hipótese alternativa:	-0,5 < Diferença < 0,5
Nível α:	0,05

Hipótese Nula	GL	Valor-T	Valor-p
Diferença ≤ -0,5	13	3,3657	0,003
Diferença ≥ 0,5	13	-5,4748	0,000

Exemplo de Teste de equivalência com dados pareados

Interpretar os resultados

Método

Estatísticas Descritivas

Diferença: Média(Nova) - Média(Marca Líder)

Teste