Neste tópico
Diferença (D)
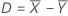
Notação
| Termo | Descrição |
|---|---|
| D | Diferença |
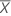 | Média do teste |
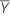 | Média de referência |
Médias e desvios padrão
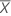 , é dada por:
, é dada por:
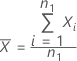
A média da amostra de referência, 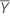 , é dada por:
, é dada por:
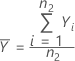
O desvio padrão da amostra de teste, S1, é dado por:
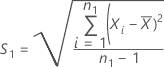
O desvio padrão da amostra de referência, S2, é dado por:
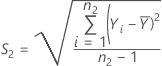
Notação
| Termo | Descrição |
|---|---|
| X i | Observações a partir da amostra de teste, com i = 1, ..., n1 |
| Y i | Observações a partir da amostra de referência, com i = 1, ..., n2 |
| n1 | Número de observações na amostra de teste |
| n2 | Número de observações na amostra de referência |
Erro padrão da diferença (SE)
Não assuma variâncias iguais (padrão)

Assumir variâncias iguais
Se você selecionar a opção para assumir variâncias iguais, o Minitab calcula o desvio padrão combinado, Sp, e o erro padrão da diferença, SE, usando as seguintes fórmulas:
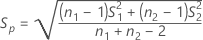
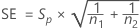
Notação
| Termo | Descrição |
|---|---|
| S1 | Desvio padrão da amostra de teste |
| n1 | Número de observações na amostra de teste |
| S2 | Desvio padrão da amostra de referência |
| n2 | Número de observações na amostra de referência |
| Sp | Desvio padrão combinado |
Limites de equivalência
Permita que k1 seja o valor especificado para limite inferior e k2 seja o valor especificado para limite superior. Por padrão, o limite de equivalência inferior, δ1, é dado por:

e o limite de equivalência superior, δ2, é dado por:
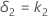
Graus de liberdade (DF)
Não assuma variâncias iguais (padrão)
Por padrão, os graus de liberdade para o teste, v, são dados pela seguinte fórmula:
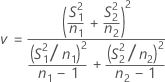
O Minitab exibe v arredondado para o número inteiro mais próximo.
Assumir variâncias iguais
Se você selecionar a opção para assumir variâncias iguais, o Minitab calcula os graus de liberdade da seguinte forma:

Notação
| Termo | Descrição |
|---|---|
| S1 | Desvio padrão da amostra de teste |
| n1 | Número de observações na amostra de teste |
| S2 | Desvio padrão da amostra de referência |
| n2 | Número de observações na amostra de referência |
Intervalo de confiança
100(1-α)% do IC
Por padrão, o Minitab usa a seguinte fórmula para calcular o intervalo de confiança (IC) de 100(1 – α)% para equivalência:
IC = [min(C, Dl), max(C, Du)]
em que:

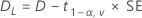
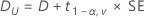
100(1-2α)% de IC
Se você selecionar a opção para usar o 100(1 - 2α)% de IC, o IC é dado pela seguinte fórmula:
IC = [Dl, Du]
Intervalos unilaterais
Para uma hipótese de Média de teste > média de referência ou Média de teste - média de referência > limite inferior, o limite inferior de 100(1 – α)% é igual a DL.
Para uma hipótese de Média de teste < média de referência ou Média de teste - média de referência < limite superior, o limite superior de 100(1 – α)% é igual a DU.Notação
| Termo | Descrição |
|---|---|
| D | A diferença entre a média de teste e a média de referência |
| SE | Erro padrão |
| δ1 | Limite de equivalência inferior |
| δ2 | Limite de equivalência superior |
| v | Graus de liberdade |
| α | O nível de significância para o teste (alfa) |
| t1-α, v | O valor crítico 1 - α superior para uma distribuição de t com v graus de liberdade |
Valores T
 , e permita que t 2 seja o valor de t para a hipótese,
, e permita que t 2 seja o valor de t para a hipótese,  , em que
, em que  é a diferença entre a média da população de teste e a média da população de referência. Por padrão, os valores de t são calculados da seguinte forma:
é a diferença entre a média da população de teste e a média da população de referência. Por padrão, os valores de t são calculados da seguinte forma:


Para a hipótese de Média de teste > média de referência, δ1= 0.
Para a hipótese de Média de teste < média de referência, δ2= 0.
Notação
| Termo | Descrição |
|---|---|
| D | A diferença entre a média de teste da amostra e a média de referência da amostras |
| SE | Erro padrão da diferença |
| δ1 | Limite de equivalência inferior |
| δ2 | Limite de equivalência superior |
Valores de p
| H0 | Valor de P |
|---|---|
 |
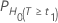 |
 |
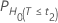 |
Notação
| Termo | Descrição |
|---|---|
 | Diferença desconhecida entre a média da população de teste e a média da população de referência |
| δ1 | Limite de equivalência inferior |
| δ2 | Limite de equivalência superior |
| v | Graus de liberdade |
| T | distribuição de t com v graus de liberdade |
| t1 | valor de t para a hipótese  |
| t2 | valor de t para a hipótese  |
Observação
Para obter informações sobre como os valores de t são calculados, consulte a seção sobre valores de t.
