Gráfico de equivalência
Um gráfico de equivalência exibe os limites de equivalência, o intervalo de confiança para equivalência, e a decisão sobre se você pode afirmar equivalência.
Interpretação
Use o gráfico de equivalência para exibir um resumo gráfico dos resultados do teste de equivalência e para determinar se pode afirmar equivalência.
Compare o intervalo de confiança com os limites de equivalência. Se o intervalo de confiança estiver completamente dentro dos limites de equivalência, você poderá afirmar que a média da população do teste é equivalente à média da população de referência. Se parte do intervalo de confiança estiver fora dos limites de equivalência, você não poderá afirmar a equivalência.
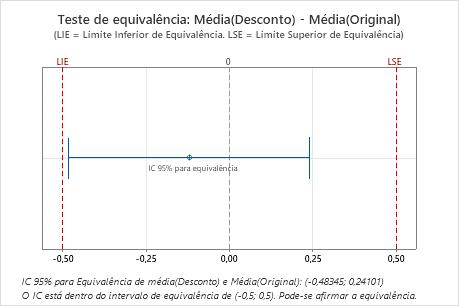
Nesses resultados, o intervalo de confiança de 95% está completamente dentro do intervalo de equivalência definido pelo limite equivalência inferior (LEL) e pelo limite de equivalência superior (UEL). Portanto, você pode concluir que a média do teste é equivalente à média de referência.
Histograma
Um histograma divide os valores amostrais em diversos intervalos e representa a frequência dos valores de dados em cada intervalo com uma barra.
Interpretação
Use histogramas para avaliar a forma e a dispersão dos dados. Os histogramas são melhores quando o tamanho amostral é maior do que 20.
- Dados assimétricos
-
Determine se seus dados parecem ser assimétricos.quando os dados estão assimétricos, a maior parte dos dados está voltada para o lado alto ou baixo do gráfico. Com frequência, a assimetria é mais fácil de identificar com um boxplot ou histograma.
Assimétricos à direita
Assimétricos à esquerda
Por exemplo, o histograma assimétrico à direita mostra dados salariais. A muitos funcionários é paga uma quantidade relativamente pequena, enquanto, cada vez mais, a poucos funcionários são pagos grandes salários. O histograma assimétrico à esquerda mostra dados de taxa de falha. Alguns itens falham antes enquanto um número crescente de itens falham mais tarde.
Os dados que são severamente assimétricos podem afetar a validade dos resultados do teste se sua amostra for muito pequena (< 20 valores). Se seus dados forem severamente assimétricos e você tiver uma pequena amostra, considere aumentar o tamanho amostral.
- Outliers
-
Outliers, que são pontos de dados que estão longe da maioria dos outros dados, podem afetar fortemente os resultados. Os outliers são facilmente identificados em um boxplot.
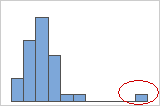
Em um histograma, barras isoladas nas extremidades sugerem possíveis outliers.
Você deve tentar identificar a causa de qualquer outliers. Corrija os erros de entrada de dados ou de medição. Considere remover os dados que estão associados a causas especiais e repetir a análise. Para obter mais informações sobre causas especiais, acesse Usando cartas de controle para detectar variação de causa comum e variação de causa especial.
Gráfico de valores individuais
Um gráfico de valores individuais exibe os valores individuais na amostra em uma coluna horizontal. Cada círculo representa uma observação. Um gráfico de valores individuais é útil quando você tiver relativamente poucas observações e desejar avaliar o efeito de cada observação.
Interpretação
- Dados assimétricos
-
Determine se seus dados parecem ser assimétricos.quando os dados estão assimétricos, a maior parte dos dados está voltada para o lado alto ou baixo do gráfico. Com frequência, a assimetria é mais fácil de identificar com um boxplot ou histograma.
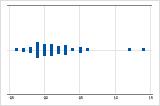
Assimétricos à direita
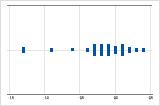
Assimétricos à esquerda
Por exemplo, o gráfico do valor individual assimétrico à direita mostra dados salariais. A muitos funcionários é paga uma quantidade relativamente pequena, enquanto, cada vez mais, a poucos funcionários são pagos grandes salários. O gráfico de valor individual assimétrico à esquerda mostra a taxa de falha de dados. Alguns itens falham antes enquanto um número crescente de itens falham mais tarde.
Os dados que são severamente assimétricos podem afetar a validade dos resultados do teste se sua amostra for muito pequena (< 20 valores). Se seus dados forem severamente assimétricos e você tiver uma pequena amostra, considere aumentar o tamanho amostral.
- Outliers
-
Outliers, que são pontos de dados que estão longe da maioria dos outros dados, podem afetar fortemente os resultados. Os outliers são facilmente identificados em um boxplot.
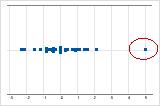
Em um gráfico de valores individuais, valores de dados atipicamente altos ou baixos sugerem possíveis outliers.
Você deve tentar identificar a causa de qualquer outliers. Corrija os erros de entrada de dados ou de medição. Considere remover os dados que estão associados a causas especiais e repetir a análise. Para obter mais informações sobre causas especiais, acesse Usando cartas de controle para detectar variação de causa comum e variação de causa especial.
Boxplot
O boxplot fornece um resumo gráfico da distribuição de cada amostra que mostra sua forma, a tendência central e a variabilidade. Isso permite uma comparação fácil dos grupos.
Interpretação
Use um boxplot para examinar a dispersão dos dados e identificar quaisquer outliers potenciais. Os boxplots são melhores quando o tamanho amostral for superior a 20.
- Dados assimétricos
-
Determine se seus dados parecem ser assimétricos.quando os dados estão assimétricos, a maior parte dos dados está voltada para o lado alto ou baixo do gráfico. Com frequência, a assimetria é mais fácil de identificar com um boxplot ou histograma.
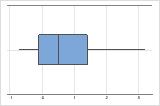
Assimétricos à direita
Assimétricos à esquerda
Por exemplo, o histograma assimétrico à direita mostra dados salariais. A muitos funcionários é paga uma quantidade relativamente pequena, enquanto, cada vez mais, a poucos funcionários são pagos grandes salários. O histograma com dados assimétricos à esquerda mostra a taxa de falha de dados. Alguns itens falham antes enquanto um número crescente de itens falham mais tarde.
Os dados que são severamente assimétricos podem afetar a validade dos resultados do teste se sua amostra for muito pequena (< 20 valores). Se seus dados forem severamente assimétricos e você tiver uma pequena amostra, considere aumentar o tamanho amostral.
- Outliers
-
Outliers, que são pontos de dados que estão longe da maioria dos outros dados, podem afetar fortemente os resultados. Os outliers são facilmente identificados em um boxplot.
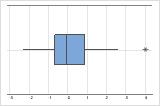
Em um boxplot, os outliers são identificados por asteriscos (*).
Você deve tentar identificar a causa de qualquer outliers. Corrija os erros de entrada de dados ou de medição. Considere remover os dados que estão associados a causas especiais e repetir a análise. Para obter mais informações sobre causas especiais, acesse Usando cartas de controle para detectar variação de causa comum e variação de causa especial.
- Igualdade de variâncias (opcional)
-
Comparar a dispersão dos dados
Por padrão, o teste de equivalência não assume que as variâncias de cada grupo são iguais. Contudo, se você selecionar a opção Assumir variâncias iguais do teste, compare os gráficos de cada grupo para garantir que a dispersão dos dados é similar. Se a dispersão difere substancialmente, você não deve assumir variâncias iguais quando realizar o teste.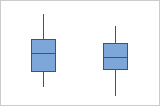
Observação
Para verificar formalmente as variâncias iguais, use o teste para Teste para 2 variâncias .
