Exemplo de Teste de equivalência para 2 amostra

Um engenheiro alimentício de uma empresa de alimentos para animais domésticos testa uma nova fórmula mais barata de sua popular comida para gatos. O engenheiro quer assegurar que o conteúdo proteico da fórmula mais barata seja igual ao conteúdo proteico do alimento original. O engenheiro mede a quantidade de proteína em amostras de 100 gramas de ambas as fórmulas do alimento para verificar se ela equivale a ±0,5 gramas.

O engenheiro realiza um teste de equivalência para 2 amostras para determinar se a diferença média em proteína entre as duas formulações está dentro de ±0,5 g. O engenheiro não save se as variâncias do conteúdo de proteína são iguais para as duas formulações.

Abra os dados amostrais, ProteínaRaçãoGatos.MTW.
Selecione Estat > Testes de equivalência > 2 amostras.
Na lista suspensa, selecione Amostras em colunas diferentes.
Em Amostra de teste, insira Desconto.
Em Amostra de referência, insira Original.
Em Hipótese sobre, selecione Média de teste - média de referência.
Em O que você deseja determinar? (Hipótese alternativa), selecione Limite inferior < média de teste - média de referência < limite superior.
Em Limite inferior, insira –0,5.
Em Limite superior, insira 0,5.
Clique em OK.

Interpretar os resultados

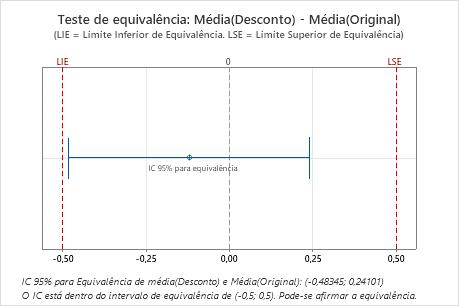
Como o intervalo de confiança está completamente dentro do intervalo de equivalência, o engenheiro conclui que as duas formulações de alimentos para gatos contêm quantidades equivalentes de proteína.

Variável	N	Média	DesvPad	EP Média
Desconto	10	33,971	0,58064	0,18361
Original	9	34,092	0,26138	0,087127

Hipótese nula:	Diferença ≤ -0,5 ou Diferença ≥ 0,5
Hipótese alternativa:	-0,5 < Diferença < 0,5
Nível α:	0,05

Hipótese Nula	GL	Valor-T	Valor-p
Diferença ≤ -0,5	12	1,8637	0,044
Diferença ≥ 0,5	12	-3,0566	0,005

Exemplo de Teste de equivalência para 2 amostra

Interpretar os resultados

Método

Estatísticas Descritivas

Diferença: Média(Desconto) - Média(Original)

Teste