Neste tópico
Diferença
A diferença é a diferença entre a média da amostra e o alvo.
Interpretação
A diferença de seus dados de amostra fornece uma estimativa da diferença entre a média da população e o alvo.
Como a diferença é baseado em dados de amostra e não em toda a população, não é possível ter certeza de que ela é igual à diferença entre a média da população e o alvo. Para avaliar a precisão da estimativa para a população, você pode usar um intervalo de confiança.
SE
O erro padrão da diferença (SE) estima a variabilidade da diferença entre o alvo e a média da amostra que você poderia obter caso extraísse repetidas amostras da mesma população. Considerando-se que o erro padrão da diferença estima a variabilidade entre as amostras, o desvio padrão mede a variabilidade dentro de uma única amostra.
Interpretação
Use o erro padrão da diferença para determinar o quão precisamente a diferença entre a média da amostra e o alvo estima a diferença entre a média da população e o alvo.
Os valores mais baixos do erro padrão indicam uma estimativa mais precisa. Normalmente, um desvio padrão maior resulta em um erro padrão maior da diferença e em uma estimativa menos precisa. Um tamanho amostral maior resulta em um erro padrão menor da diferença e uma estimativa mais precisa.
O Minitab utiliza o erro padrão da diferença para calcular a estatística de teste (valor de t).
Intervalo de confiança (IC)
O intervalo de confiança fornece um intervalo de valores prováveis para a diferença entre a média da população e o alvo. O limite inferior de confiança define um valor que provavelmente é maior que a diferença. O limite superior de confiança define um valor que provavelmente é menor que a diferença.
Observação
Se executar um teste de equivalência usando as configurações default, o Minitab exibe um intervalo de confiança para equivalência. Se alterar as configurações default e usar o método alternativo para calcular o intervalo de confiança, o Minitab exibe o intervalo padrão de confiança. Para obter informações sobre a diferença entre esses intervalos, vá para Intervalos de confiança em teste de equivalência.
Interpretação
Compare o intervalo de confiança com os limites de equivalência. Se o intervalo de confiança está completamente dentro dos limites de equivalência, você pode afirmar que a média populacional é equivalente ao alvo. Se parte do intervalo de confiança estiver fora dos limites de equivalência, você não poderá afirmar a equivalência.
Diferença: Média(Força) - Alvo
| Diferença | EP | IC 95% para equivalência | Intervalo de Equivalência |
|---|---|---|---|
| 0,28500 | 0,13831 | (0; 0,520586) | (-0,42; 0,42) |
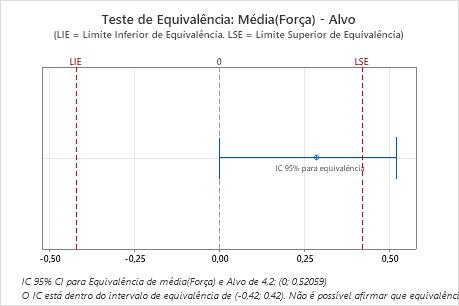
Nesses resultados, o intervalo de confiança de 95% excede o limite de equivalência superior. Portanto, você não pode afirmar que a média da população é equivalente ao alvo.
Limite inferior
O Minitab exibirá um limite inferior de confiança se você selecionar uma hipótese alternativa que inclui apenas um limite superior para a diferença. O limite inferior indica um valor contra o qual a diferença entre a média da população e o alvo apresenta probabilidade de ser maior.
Interpretação
Utilize o limite inferior de confiança para determinar se a diferença entre a média da população e o alvo é maior do que o limite inferior. Se o limite de confiança inferior for maior do que o limite inferior, é possível afirmar que a diferença entre a média da população e o alvo é maior do que o limite inferior.
Diferença: Média(Força) - Alvo
| Diferença | EP | Unilateral è Esquerda de 95% | Limite Inferior |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,049414 | -0,42000 |
Nestes resultados, o limite inferior de confiança de 95% para a diferença é 0,04914, que é maior do que o limite inferior de −0,4200. Portanto, é possível ter 95% de confiança que a diferença entre a média da população e o alvo é maior do que limite inferior.
Limite superior
O Minitab exibirá um limite superior de confiança se você selecionar uma hipótese alternativa que inclui apenas um limite superior para a diferença. O limite superior indica um valor contra o qual a diferença entre a média da população e o alvo apresenta probabilidade de ser menor.
Interpretação
Utilize o limite superior de confiança para determinar se a diferença entre a média da população e o alvo é menor que o limite superior. Se o limite de confiança superior for menor do que o limite superior, é possível afirmar que a diferença entre a média da população e o alvo é menor do que o limite superior.
Diferença: Média(Força) - Alvo
| Diferença | EP | Limite superior de 95% | Limite Superior |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,52059 | 0,42000 |
Nestes resultados, a confiança superior de 95% de ligação é 0,52059, que é maior do que o limite superior de 0,4200. Portanto, não é possível afirmar que a diferença entre a média da população e o alvo seja menor do que o limite superior.
Intervalo de equivalência
Um intervalo de equivalência é um intervalo de valores que estão próximos o suficiente da meta para serem considerados equivalentes. O intervalo é baseado em seu conhecimento do produto ou processo e é definido por um limite inferior de equivalência (LEL) e um limite superior de equivalência (UEL).
Interpretação
Compare o intervalo de confiança com os limites de equivalência. Se o intervalo de confiança está completamente dentro dos limites de equivalência, você pode afirmar que a média populacional é equivalente ao alvo. Se parte do intervalo de confiança estiver fora dos limites de equivalência, você não poderá afirmar a equivalência.
Diferença: Média(Força) - Alvo
| Diferença | EP | IC 95% para equivalência | Intervalo de Equivalência |
|---|---|---|---|
| 0,28500 | 0,13831 | (0; 0,520586) | (-0,42; 0,42) |

Nesses resultados, o intervalo de confiança de 95% excede o limite de equivalência superior. Portanto, você não pode afirmar que a média da população é equivalente ao alvo.
Limite inferior
O limite inferior de aceitabilidade para a diferença entre a média e o alvo. Você deseja que a diferença entre a média da população de teste e o alvo sejam maiores do que o limite inferior.
Interpretação
Compare o limite inferior com o limite de confiança inferior. Se o limite de confiança inferior for maior do que o limite inferior, é possível afirmar que a diferença entre a média da população e o alvo é maior do que o limite inferior.
Diferença: Média(Força) - Alvo
| Diferença | EP | Unilateral è Esquerda de 95% | Limite Inferior |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,049414 | -0,42000 |
Nestes resultados, o limite inferior de confiança de 95% para a diferença é 0,04914, que é maior do que o limite inferior de −0,4200. Portanto, é possível ter 95% de confiança que a diferença entre a média da população e o alvo é maior do que limite inferior.
Limite superior
O limite superior de aceitabilidade para a diferença entre a média e o alvo. Você deseja que a diferença entre a média da população de teste e o alvo sejam menores do que o limite superior.
Interpretação
Compare o limite superior com o limite de confiança superior. Se o limite de confiança superior for menor do que o limite superior, é possível afirmar que a diferença entre a média da população e o alvo é menor do que o limite superior.
Diferença: Média(Força) - Alvo
| Diferença | EP | Limite superior de 95% | Limite Superior |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,52059 | 0,42000 |
Nestes resultados, a confiança superior de 95% de ligação é 0,52059, que é maior do que o limite superior de 0,4200. Portanto, não é possível afirmar que a diferença entre a média da população e o alvo seja menor do que o limite superior.
