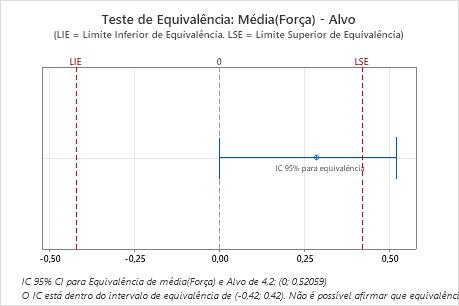
Exemplo de Teste de equivalência para 1 amostra

Um engenheiro de embalagens quer testar um novo método para vedar pacotes de salgadinhos. A força necessária para abrir os sacos deve estar dentro de 10% do valor da meta de 4,2 N (Newtons). O engenheiro seleciona, aleatoriamente, 28 sacos de amostra que estão vedados usando o novo método e registra a força necessária para abrir cada saco.

O engenheiro realiza um teste de equivalência para 1 amostra para determinar se a força média necessária para abrir os sacos com o novo método de vedação está dentro de 10% da meta de 4,2N.

Abra os dados amostrais, VedaçãoDePacoteDeSalgadinhos.MTW.
Selecione Estat > Testes de equivalência > 1 amostra.
Na lista suspensa, selecione Amostra em uma coluna.
Em Amostra, insira Força.
Em Alvo, insira 4,2.
Em O que você deseja determinar? (Hipótese alternativa), selecione Limite inferior < média de teste - alvo < limite superior.
Em Limite inferior, insira –0,1.
Em Limite superior, insira 0,1.
Selecione Multiplicar pelo alvo.
Clique em OK.

Interpretar os resultados

O intervalo de confiança não está completamente dentro do intervalo de equivalência. Por isso, o engenheiro não pode afirmar que a força necessária para abrir os sacos com o novo selo é equivalente à meta de 4,2 N.

Hipótese nula:	Diferença ≤ -0,42 ou Diferença ≥ 0,42
Hipótese alternativa:	-0,42 < Diferença < 0,42
Nível α:	0,05

Hipótese Nula	GL	Valor-T	Valor-p
Diferença ≤ -0,42	27	5,0972	0,000
Diferença ≥ 0,42	27	-0,97605	0,169

Exemplo de Teste de equivalência para 1 amostra

Interpretar os resultados

Método

Estatísticas Descritivas

Diferença: Média(Força) - Alvo

Teste